
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
北京时间2011年3月11日,日本近海发生9.0级强烈地震.本次地震导致地球当天自转快了0.000 001 6秒.这里的0.000 001 6秒用科学记数法表示__________秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
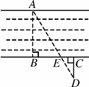
如图6414,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20 m,EC=10 m,CD=20 m,则河的宽度AB=( )
A. 60 m B. 40 m C. 30 m D. 20 m
查看答案和解析>>
科目:初中数学 来源: 题型:
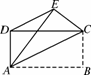
如图6117,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE∶AC=3∶5,则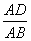 的值为( )
的值为( )
A.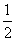 B.
B.  C.
C.  D.
D. 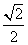
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)观察发现.
如图6124(1):若点A,B在直线m的同侧,在直线m上找一点P,使AP+BP的值最小,做法如下:作点B关于直线m的对称点B′,连接AB′,与直线m的交点就是所求的点P,线段AB′的长度即为AP+BP的最小值.
如图6124(2):在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小,做法如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点.则这就是所求的点P,故BP+PE的最小值为__________________.
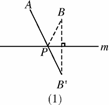
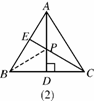
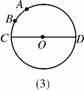

图6124
(2)实践运用.
如图6124(3):已知⊙O的直径CD为2,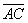 的度数为60°,点B是
的度数为60°,点B是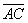 的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的最小值为________________.
的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的最小值为________________.
(3)拓展延伸.
如图6124(4):点P是四边形ABCD内一点,分别在边AB,BC上作出点M,N,使PM+PN的值最小,保留作图痕迹,不写作法.
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)如图1的图形我们把它称为“8字形”,请说明 ;
;
(2)阅读下面的内容,并解决后面的问题:
如图2, 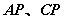 分别平分
分别平分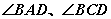 ,
,
若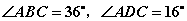 ,求
,求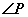 的度数;
的度数;
解:∵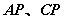 分别平分
分别平分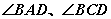 ∴
∴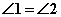 ,
,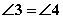
由(1)的结论得: 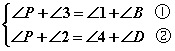
①+②,得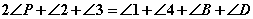
∴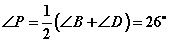 .
.
① 如图3, 直线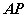 平分
平分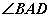 的外角
的外角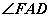 ,
,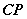 平分
平分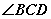 的外角
的外角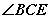 ,
,
若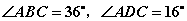 ,求
,求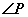 的度数;
的度数;
② 在图4中,直线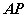 平分
平分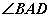 的外角
的外角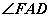 ,
,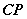 平分
平分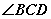 的外角
的外角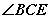 ,猜想
,猜想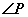 与
与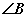 、
、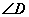 的关系,直接写出结论,无需说明理由.
的关系,直接写出结论,无需说明理由.
③ 在图5中,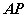 平分
平分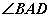 ,
,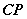 平分
平分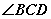 的外角
的外角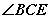 ,猜想
,猜想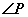 与
与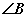 、
、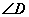 的关系,直接写出结论,无需说明理由.
的关系,直接写出结论,无需说明理由.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com