
 在梯形ABDC中,AB∥CD,对角线AD交BC于点O,OA:OD=1:2,则下列结论:
在梯形ABDC中,AB∥CD,对角线AD交BC于点O,OA:OD=1:2,则下列结论:
① ,②CD=2AB,③S△OCD=2S△OAB,④S△ABC=3S△OAB;
,②CD=2AB,③S△OCD=2S△OAB,④S△ABC=3S△OAB;
其中正确的结论是
 ,②CD=2AB,由相似三角形的面积比等于相似比的平方,即可得S△OCD=4S△OAB,由等高三角形的面积比等于对应底的比,即可求得S△ABC=3S△OAB.
,②CD=2AB,由相似三角形的面积比等于相似比的平方,即可得S△OCD=4S△OAB,由等高三角形的面积比等于对应底的比,即可求得S△ABC=3S△OAB.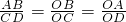 =
= ,
,

 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:

| AB |
| DC |
| BE |
| EC |
查看答案和解析>>
科目:初中数学 来源: 题型:
 在梯形ABDC中,AB∥CD,对角线AD交BC于点O,OA:OD=1:2,则下列结论:①
在梯形ABDC中,AB∥CD,对角线AD交BC于点O,OA:OD=1:2,则下列结论:①| OB |
| OC |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(广东珠海卷)数学(带解析) 题型:解答题
如图,在等腰梯形ABCD中,ABDC,AB=3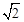 ,DC=
,DC=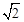 ,高CE=2
,高CE=2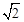 ,对角线AC、BD交于H,平行于线段BD的两条直线MN、RQ同时从点A出发沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G;当直线RQ到达点C时,两直线同时停止移动.记等腰梯形ABCD被直线MN扫过的图形面积为S1、被直线RQ扫过的图形面积为S2,若直线MN平移的速度为1单位/秒,直线RQ平移的速度为2单位/秒,设两直线移动的时间为x秒.
,对角线AC、BD交于H,平行于线段BD的两条直线MN、RQ同时从点A出发沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G;当直线RQ到达点C时,两直线同时停止移动.记等腰梯形ABCD被直线MN扫过的图形面积为S1、被直线RQ扫过的图形面积为S2,若直线MN平移的速度为1单位/秒,直线RQ平移的速度为2单位/秒,设两直线移动的时间为x秒.
(1)填空:∠AHB= ;AC= ;
(2)若S2=3S1,求x;
(3)设S2=mS1,求m的变化范围.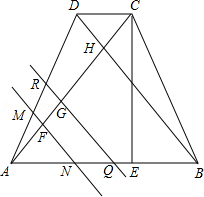
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(广东珠海卷)数学(解析版) 题型:解答题
如图,在等腰梯形ABCD中,ABDC,AB=3 ,DC=
,DC= ,高CE=2
,高CE=2 ,对角线AC、BD交于H,平行于线段BD的两条直线MN、RQ同时从点A出发沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G;当直线RQ到达点C时,两直线同时停止移动.记等腰梯形ABCD被直线MN扫过的图形面积为S1、被直线RQ扫过的图形面积为S2,若直线MN平移的速度为1单位/秒,直线RQ平移的速度为2单位/秒,设两直线移动的时间为x秒.
,对角线AC、BD交于H,平行于线段BD的两条直线MN、RQ同时从点A出发沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G;当直线RQ到达点C时,两直线同时停止移动.记等腰梯形ABCD被直线MN扫过的图形面积为S1、被直线RQ扫过的图形面积为S2,若直线MN平移的速度为1单位/秒,直线RQ平移的速度为2单位/秒,设两直线移动的时间为x秒.
(1)填空:∠AHB= ;AC= ;
(2)若S2=3S1,求x;
(3)设S2=mS1,求m的变化范围.
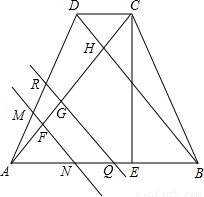
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com