
分析 先根据已知得出x-y-5=0,xy+6=0,求出x、y的值,再求出x+y、x+2y、x-2y的值,分别代入求出即可.
解答 解:∵(x-y-5)2014+(xy+6)2016=0,
∴x-y-5=0,xy+6=0,
解得:$\left\{\begin{array}{l}{{x}_{1}=-2}\\{{y}_{1}=3}\end{array}\right.$或$\left\{\begin{array}{l}{{x}_{2}=-3}\\{{y}_{2}=2}\end{array}\right.$,
①当x=-2,y=3时,
x+y=1,x+2y=4,x-2y=-8,
(x+2y-1)2+(x-2y)(x+y)-2(x+y)
=(4-1)2+(-8)×1-2×1=-1;
②当x=-3,y=2时,
x+y=-1,x+2y=1,x-2y=-7,
(x+2y-1)2+(x-2y)(x+y)-2(x+y)
=(1-1)2+(-7)×(-1)-2×(-1)=9.
点评 本题考查了整式的混合运算和求值的应用,能求出x、y的值是解此题的关键,用了整体代入思想.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题
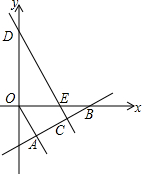 如图,直线y=$\frac{1}{2}$x-$\frac{11}{2}$与x轴交于B,与直线y=-$\frac{4}{3}$x相交于A,线段AB的垂直平分线CD分别与AB,x轴,y轴交于点C,E,D.
如图,直线y=$\frac{1}{2}$x-$\frac{11}{2}$与x轴交于B,与直线y=-$\frac{4}{3}$x相交于A,线段AB的垂直平分线CD分别与AB,x轴,y轴交于点C,E,D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
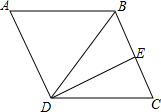 如图,平行四边形ABCD中,∠ABC>∠A,E为BC边的中点,连接BD、ED,∠CDE=30°,∠ADB=∠BDE=2:1,则∠A=60°.
如图,平行四边形ABCD中,∠ABC>∠A,E为BC边的中点,连接BD、ED,∠CDE=30°,∠ADB=∠BDE=2:1,则∠A=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com