
 如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )
如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )| A. | ①② | B. | ②③④ | C. | ①②④ | D. | ①②③④ |
分析 由在平行四边形ABCD中,AD=2AB,F是AD的中点,易得AF=FD=CD,继而证得①∠DCF=$\frac{1}{2}$∠BCD;然后延长EF,交CD延长线于M,分别利用平行四边形的性质以及全等三角形的判定与性质得出△AEF≌△DMF(ASA),得出对应线段之间关系进而得出答案.
解答 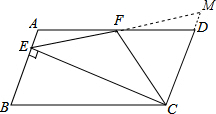 解:①∵F是AD的中点,
解:①∵F是AD的中点,
∴AF=FD,
∵在?ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠DCF=$\frac{1}{2}$∠BCD,故此选项正确;
②延长EF,交CD延长线于M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,
$\left\{\begin{array}{l}{∠A=∠FDM}\\{AF=DF}\\{∠AFE=∠DFM}\end{array}\right.$,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=FM,故②正确;
③∵EF=FM,
∴S△EFC=S△CFM,
∵MC>BE,
∴S△BEC<2S△EFC
故S△BEC=2S△CEF错误;
④设∠FEC=x,则∠FCE=x,
∴∠DCF=∠DFC=90°-x,
∴∠EFC=180°-2x,
∴∠EFD=90°-x+180°-2x=270°-3x,
∵∠AEF=90°-x,
∴∠DFE=3∠AEF,故此选项正确.
故选C.
点评 此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,得出△AEF≌△DME是解题关键.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
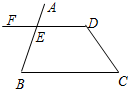 如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.
如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它是三次三项式 | B. | 它是四次两项式 | ||
| C. | 它的最高次项是-6x2yz | D. | 它的常数项是1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
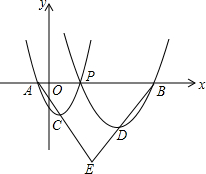 如图,已知点A(-1,0),B(7,0),P是线段AB上任意一点(不含端点A,B),过A、P两点的二次函数y1和过P、B两点的二次函数y2的图象开口均向上,它们的顶点分别为C、D,射线BD与AC相交于点E.当AE=BE=5时,这两个二次函数的最小值之和等于( )
如图,已知点A(-1,0),B(7,0),P是线段AB上任意一点(不含端点A,B),过A、P两点的二次函数y1和过P、B两点的二次函数y2的图象开口均向上,它们的顶点分别为C、D,射线BD与AC相交于点E.当AE=BE=5时,这两个二次函数的最小值之和等于( )| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$-$\sqrt{2}$ | B. | $\frac{\sqrt{2}+1}{2}$ | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com