
【题目】如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+2|+ ![]() =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3). 
(1)求a,b的值及S△ABC;
(2)若点M在x轴上,且S△ACM= ![]() S△ABC , 试求点M的坐标.
S△ABC , 试求点M的坐标.
【答案】
(1)解:∵|a+2|+ ![]() =0,
=0,
∴a+2=0,b﹣4=0,
∴a=﹣2,b=4,
∴点A(﹣2,0),点B(4,0).
又∵点C(0,3),
∴AB=|﹣2﹣4|=6,CO=3,
∴S△ABC= ![]() ABCO=
ABCO= ![]() ×6×3=9
×6×3=9
(2)解:设点M的坐标为(x,0),则AM=|x﹣(﹣2)|=|x+2|,
又∵S△ACM= ![]() S△ABC,
S△ABC,
∴ ![]() AMOC=
AMOC= ![]() ×9,
×9,
∴ ![]() |x+2|×3=3,
|x+2|×3=3,
∴|x+2|=2,
即x+2=±2,
解得:x=0或﹣4,
故点M的坐标为(0,0)或(﹣4,0)
【解析】(1)由“|a+2|+ ![]() =0”结合绝对值、算术平方根的非负性即可得出a、b的值,再结合三角形的面积公式即可求出S△ABC的值;(2)设出点M的坐标,找出线段AM的长度,根据三角形的面积公式结合S△ACM=
=0”结合绝对值、算术平方根的非负性即可得出a、b的值,再结合三角形的面积公式即可求出S△ABC的值;(2)设出点M的坐标,找出线段AM的长度,根据三角形的面积公式结合S△ACM= ![]() S△ABC , 即可得出AM的值,从而得出点M的坐标.
S△ABC , 即可得出AM的值,从而得出点M的坐标.
【考点精析】本题主要考查了三角形的面积的相关知识点,需要掌握三角形的面积=1/2×底×高才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.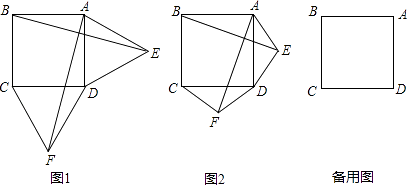
(1)请判断:AF与BE的数量关系是 , 位置关系是;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予说明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下列线段为边,能组成直角三角形的是( )
A.6cm,12cm,14cm
B.![]() cm,1cm,
cm,1cm, ![]() cm
cm
C.1.5cm,2cm,2.5cm
D.2cm,3cm,5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=DC=5,点P在BC上移动,则当PA+PD取最小值时,BP长为( )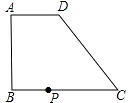
A.1
B.2
C.2.5
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果x=3m+1,y=2+9m,那么用x的代数式表示y为( )
A. y=2x B. y=x2 C. y=(x﹣1)2+2 D. y=x2+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)
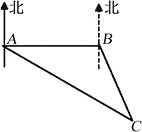
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两块相同的三角板完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,A′C′与AB相交于点D,则C′D= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() AE2;④∠DFE=2∠DAC ;⑤若连接CH,则CH∥EF.其中正确的个数为( )
AE2;④∠DFE=2∠DAC ;⑤若连接CH,则CH∥EF.其中正确的个数为( )
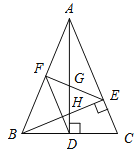
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com