
 与A,B重合),且保持DE∥BC,以DE为边,在点A的异侧作正方形DEFG.
与A,B重合),且保持DE∥BC,以DE为边,在点A的异侧作正方形DEFG.| DE |
| BC |
| AN |
| AM |
| DE |
| 12 |
| 8-DE |
| 8 |

| DE |
| BC |
| AN |
| AM |
| x |
| 12 |
| 8-EP |
| 8 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 8 | ||
2×(-
|
| 2 |
| 3 |


科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
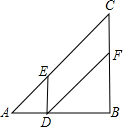 DE∥BC,DF∥AC.
DE∥BC,DF∥AC.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 的一动点,Q是边BC上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F,则△PEF面积最大值是______.
的一动点,Q是边BC上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F,则△PEF面积最大值是______.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.“抛掷一枚普通骰子出现1点朝上”的机会 |
| B.“抛掷一枚啤酒瓶盖出现盖面朝上”的机会 |
| C.“抛掷一枚质地均匀的硬币出现正面朝上”的机会 |
| D.“抛掷一枚普通图钉出现针尖触地”的机会 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 2 |
 B、C三点作⊙D.若⊙D与y轴相切.
B、C三点作⊙D.若⊙D与y轴相切.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,与y轴交点为C,连接BP并延长交y轴于点D.
,与y轴交点为C,连接BP并延长交y轴于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com