
����Ŀ����1������������ƽ������ƽ�漸�����������Ҳ�Ƿdz���Ҫ��ͼ�Σ��ڽ��ijЩƽ�漸������ʱ�����������������Ҫ������ǡ����ƽ���ߣ�������ʹ֤��˳������࣮���������˼�����̲��е����⣺��ͼ�٣�AB��CD�����B+��D�� ����E����������������������������գ���
��2���������룺д����1��������������⣬�ж����������ٲ�˵�����ɣ�
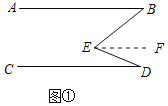
��3�����Ӧ�ã���ͼ�ڣ���֪AB��CD���ڡ�ACD��ƽ������ȡ������M��N��ʹ�á�AMN����ANM����֤����CAM����BAN��
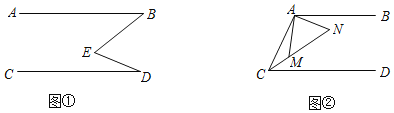
���𰸡���1��=����2������B+��D����BED����AB��CD����������Ϊ�����⣬����������3��������
��������
(1����E��EF��AB����EF��AB��CD����ƽ���ߵ����ʵó���B����BEF����D����DEF�����ɵó����ۣ�
��2����E��EF��AB�����B����BEF��֤����D����DEF���ó�EF��CD�����ɵó����ۣ�
��3������N��NG��AB����AM�ڵ�G����NG��AB��CD����ƽ���ߵ����ʵó���BAN����ANG����GNC����NCD���������ε�������ʵó���AMN����ACM+��CAM��֤����ACM+��CAM����ANG+��GNC���ó���ACM+��CAM����BAN+��NCD���ɽ�ƽ���ߵó���ACM����NCD�����ɵó����ۣ�
��1���⣺��E��EF��AB����ͼ����ʾ��
��EF��AB��CD��
���B����BEF����D����DEF��
���B+��D����BEF+��DEF��
����B+��D����BED��
�ʴ�Ϊ������
��2���⣺������Ϊ������B+��D����BED����AB��CD��
��������Ϊ�����⣻�������£�
��E��EF��AB����ͼ����ʾ��
���B����BEF��
�ߡ�B+��D����BED����BEF+��DEF����BED��
���D����BED����B����DEF����BED����BEF��
���D����DEF��
��EF��CD��
��EF��AB��
��AB��CD��
��3��֤��������N��NG��AB����AM�ڵ�G����ͼ����ʾ��
��NG��AB��CD��
���BAN����ANG����GNC����NCD��
�ߡ�AMN�ǡ�ACM��һ����ǣ�
���AMN����ACM+��CAM��
�֡ߡ�AMN����ANM����ANM����ANG+��GNC��
���ACM+��CAM����ANG+��GNC��
���ACM+��CAM����BAN+��NCD��
��CNƽ�֡�ACD��
���ACM����NCD��
���CAM����BAN��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪AB��CD��AD��BC��AC��BD���ڵ�O��AE��BD��E��CF��BD��E��ͼ��ȫ���������У�������

A. 3�� B. 5�� C. 6�� D. 7��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ɽ�����г�Խ��Խ�ܵ���ѧ����ϲ��������Ʒ�����Ͷ���г���ij���о�Ӫ��A�ͳ�ȥ�������ܶ�Ϊ5��Ԫ������ÿ�����ۼ۱�ȥ�꽵��400Ԫ����������������ͬ�������ܶ��ȥ�����20%��
��1������A�ͳ�ÿ���ۼ۶���Ԫ�������з��̵ķ������
��2���ó��мƻ��½�һ��A�ͳ����¿�B�ͳ���60������B�ͳ��Ľ�������������A�ͳ�������������Ӧ��ν�������ʹ������������ࣿ
A��B�����ͺų��Ľ��������ۼ۸����±���
A�ͳ� | B�ͳ� | |
�����۸�Ԫ�� | 1100 | 1400 |
���ۼ۸�Ԫ�� | ��������ۼ۸� | 2000 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����ij������Ʒ�ijɱ�Ϊÿ��40Ԫ�������г����з��֣������Ʒ��δ��������![]() ��
��![]() ��������
��������![]() ��
��![]() ��ʱ��
��ʱ��![]() ��
��![]() �Ĺ�ϵ��ͼ��ʾ
�Ĺ�ϵ��ͼ��ʾ![]() δ��������
�������![]() ��
��![]() ����Ʒÿ��ļ۸�
����Ʒÿ��ļ۸�![]() Ԫ
Ԫ![]() ��
��![]() ��ʱ��
��ʱ��![]() ��
��![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��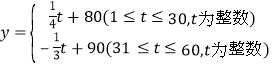
����������Ϣ������������⣺
![]() ��ֱ�ȷ��
��ֱ�ȷ��![]() ��
��![]() ʱ�ò�Ʒ��������
ʱ�ò�Ʒ��������![]() ��
��![]() ��ʱ��
��ʱ��![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
![]() ��Ԥ��δ����һ������������
��Ԥ��δ����һ������������![]() Ԫ
Ԫ![]() ����Сֵ�Ƕ��٣��ڶ���������������
����Сֵ�Ƕ��٣��ڶ���������������![]() Ԫ
Ԫ![]() �����ֵ�Ƕ��٣�
�����ֵ�Ƕ��٣�
![]() Ϊ������������ᡱ�����������������ָû�����Ʒ�����������ۣ��ӵڶ����¿�ʼÿ����һ���ò�Ʒ�Ͳ���aԪ
Ϊ������������ᡱ�����������������ָû�����Ʒ�����������ۣ��ӵڶ����¿�ʼÿ����һ���ò�Ʒ�Ͳ���aԪ![]() �������������Ժڶ������ڸò�Ʒ����������
�������������Ժڶ������ڸò�Ʒ����������![]() Ԫ
Ԫ![]() ��ʱ��
��ʱ��![]() ��
��![]() �������������a��ȡֵ��Χ��
�������������a��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() Ϊֱ��
Ϊֱ�� ![]() �ϵ�һ�㣬��
�ϵ�һ�㣬��![]() Ϊ�۲����ģ�����
Ϊ�۲����ģ�����![]() ��ʾ��������
��ʾ��������![]() ��ʾ��������
��ʾ��������![]() ��������
��������![]() ������
������![]() �ķ������ͼ��ʾ��
�ķ������ͼ��ʾ��
��1����ͼ1��ʾ���� ![]() ʱ��
ʱ��
����![]() ��������
��������![]() �ķ����� ��
�ķ����� ��
�� ![]() ��
��![]() �Ĺ�ϵΪ ��
�Ĺ�ϵΪ ��
�� ![]() ��
��![]() �Ĺ�ϵΪ ��
�Ĺ�ϵΪ ��
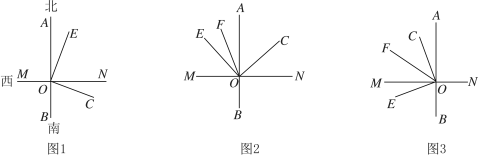
��2����������![]() ������
������![]() �Ƶ�
�Ƶ�![]() ��ת��ͼ
��ת��ͼ![]() ��λ�ã���һ������
��λ�ã���һ������![]() ǡ��ƽ��
ǡ��ƽ��![]() ����ת��ʼ�ձ���
����ת��ʼ�ձ���![]() ��
��
����![]() ����
����![]() �� .
�� .
����![]() ����
����![]() ���ú�
���ú� ![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��3����������![]() ������
������![]() �Ƶ�
�Ƶ�![]() ��ת��ͼ
��ת��ͼ![]() ��λ�ã�����
��λ�ã�����![]() ��Ȼƽ��
��Ȼƽ��![]() ����ת��ʼ�ձ���
����ת��ʼ�ձ���![]() ����
����![]() ��
��![]() ֮�����������������ϵ����˵�����ɣ�
֮�����������������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����6.26���ʽ����յ���֮�ʣ�ij�н�ίΪ���ռ�����֪ʶ����߽�����ʶ���ٰ��ˡ��ذ��������ܾ���Ʒ����֪ʶ������ijУ���꼶�����꼶�ֱ���300�ˣ��ִ��и������ȡ20��ͬѧ�IJ��Գɼ����е���������ɼ����£�
���꼶 | 68 | 88 | 100 | 100 | 79 | 94 | 89 | 85 | 100 | 88 |
100 | 90 | 98 | 97 | 77 | 94 | 96 | 100 | 92 | 67 | |
���꼶 | 69 | 97 | 91 | 69 | 98 | 100 | 99 | 100 | 90 | 100 |
99 | 89 | 97 | 100 | 99 | 94 | 79 | 99 | 98 | 79 |
��1�������������ݣ������б������.
���������������ݣ���
������ |
|
|
|
|
���꼶���� | 2 | ___________ | ___________ | 12 |
���꼶���� | 2 | 2 | 1 | 15 |
���������ݣ����������ݵ�ƽ��������λ�����±���
�꼶 | ƽ���� | ��λ�� |
���꼶 | 90.1 | 93 |
���꼶 | 92.3 | ___________ |
���ó����ۣ���
��2������Ϊ�ĸ��꼶���ս���֪ʶ������ˮƽ�Ϻã�����������˵���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OA��OB��������OC����C�ڡ�AOB�⣩������BOC������0�㣼����90�㣩��
ODƽ��BOC��OEƽ��AOD��
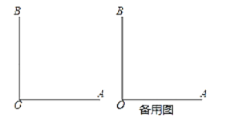
��1��������40�㣬�������ⲹȫͼ�Σ������BOE�Ķ�����
��2������ݡ�BOC�����������BOE�Ķ������ú����ı�ʾ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+4��ͼ����x�ύ������A��B����y�ύ�ڵ�C����A����1��0����B��4��0����
��1����˶��κ����ı���ʽ��
��2����ͼ1�������ߵĶԳ���m��x�ύ�ڵ�E��CD��m������ΪD����F����![]() ��0��������N���߶�DE���˶�������CF��CN��FN�����Ե�C��D��NΪ���������������FEN���ƣ����N�����ꣻ
��0��������N���߶�DE���˶�������CF��CN��FN�����Ե�C��D��NΪ���������������FEN���ƣ����N�����ꣻ
��3����ͼ2����M���������ϣ��ҵ�M�ĺ�������1��������MA�Ƶ�M��ʱ����ת45�������������ڵ�P�����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������̳�ƽʱ��ͬ���۸������ͬ����Ʒ�������ڼ������̳��������������ͼ�ǹ���ס��������̳�����Ʒ��ʵ�ʽ��![]() ��
��![]() ��Ԫ����ԭ��
��Ԫ����ԭ��![]() ��Ԫ���ĺ���ͼ������˵����ȷ���ǣ� ��
��Ԫ���ĺ���ͼ������˵����ȷ���ǣ� ��
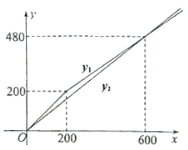
A. ��![]() ʱ��ѡ��ʡǮB. ��
ʱ��ѡ��ʡǮB. ��![]() ʱ���ס���ʵ�ʽ��һ��
ʱ���ס���ʵ�ʽ��һ��
C. ��![]() ʱ��ѡ�Ҹ�ʡǮD. ��
ʱ��ѡ�Ҹ�ʡǮD. ��![]() ʱ��ѡ��ʡǮ
ʱ��ѡ��ʡǮ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com