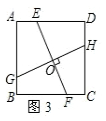
试题分析:在正方形ABDE和ACFG中,AB=AE,AC=AG,∠BAE=∠CAG=90°,
∴∠BAE+∠BAC=∠CAG+∠BAC,即∠CAE=∠BAG。
∵在△ABG和△AEC中,AB=AE,∠CAE=∠BAG,AC=AG,
∴△ABG≌△AEC(SAS),∴BG=CE。故①正确。
设BG、CE相交于点N,
∵△ABG≌△AEC,∴∠ACE=∠AGB。
∵∠NCF+∠NGF=∠ACF+∠AGF=90°+90°=180°,
∴∠CNG=360°﹣(∠NCF+∠NGF+∠F)=360°﹣(180°+90°)=90°。
∴BG⊥CE。故②正确。
过点E作EP⊥HA的延长线于P,过点G作GQ⊥AM于Q,
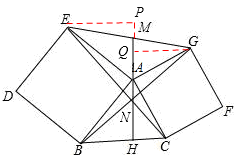
∵AH⊥BC,∴∠ABH+∠BAH=90°。
∵∠BAE=90°,∴∠EAP+∠BAH=180°﹣90°=90°。∴∠ABH=∠EAP。
∵在△ABH和△EAP中,∠ABH=∠EAP,∠AHB=∠P=90°,AB=AE,
∴△ABH≌△EAP(AAS)。∴∠EAM=∠ABC。故④正确。
∵△ABH≌△EAP,∴EP=AH。
同理可得GQ=AH。∴EP=GQ。
∵在△EPM和△GQM中,∠P=∠MQG=90°,∠EMP=∠GMQ,EP=GQ,
∴△EPM≌△GQM(AAS)。∴EM=GM。∴AM是△AEG的中线。故③正确。
综上所述,①②③④结论都正确。故选A。




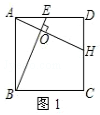
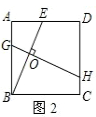
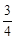 ,则BE+CE= .
,则BE+CE= .