
分析 (1)根据条形统计图和扇形统计图,即可解答;
(2)根据E段对应的人数为38人,所占的百分比为20%,即可得到样本容量;先算出D段所占的百分比,再乘以360°,即可得到圆心角的度数;
(3)根据样本估计总体,即可解答.
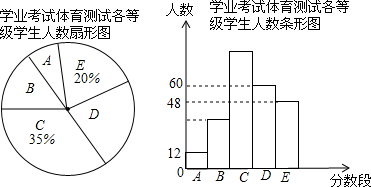
解答 解:(1)由条形统计图可得:样本中A段的人数为12人,C段人数占被调查人数的百分比为35%;
故答案为:12,35.
(2)总人数:48÷20%=240(人),所以样本容量为240;
D段人数在扇形统计图中所占圆心角的度数为:$\frac{60}{240}×36{0}^{°}=9{0}^{°}$,
故答案为:240,90;
(3)$15000×\frac{48+60}{240}$=6750,
答:估计该市学业考试体育成绩在D段和E段的总人数为6750人.
点评 本题考查利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
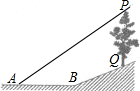 已知:如图,斜坡BQ坡度i=5:12(即为QC与BC的长度之比),在斜坡BQ上有一棵香樟树PQ,柳明在A处测得树顶点P的仰角为α,并且测得水平的AB=8米,另外BQ=13米,tanα=0.75.点A,B,P,Q在同一平面上,PQ⊥AB于点C.求香樟树PQ的高度.
已知:如图,斜坡BQ坡度i=5:12(即为QC与BC的长度之比),在斜坡BQ上有一棵香樟树PQ,柳明在A处测得树顶点P的仰角为α,并且测得水平的AB=8米,另外BQ=13米,tanα=0.75.点A,B,P,Q在同一平面上,PQ⊥AB于点C.求香樟树PQ的高度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 选手 | 甲 | 乙 | 丙 |
| 平均数 | 9.3 | 9.3 | 9.3 |
| 方差 | 0.026 | 0.015 | 0.032 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 165 | B. | 168 | C. | 170 | D. | 172 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
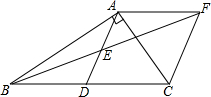 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com