
【题目】如图,在□ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.

(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠DPF的值.
【答案】(1)证明见解析(2)![]()
【解析】
试题分析:(1)利用条件先证明四边形ABEF是平行四边形,然后再证明AB=BE即可;(2)延长BF,作DH⊥PH于H,在Rt△DFH中,求出FH,DH的长,在Rt△APF中,求出PF的长,从而在Rt△PDH中,利用三角函数的定义可求tan∠DPF的值.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAE=∠AEB
∵AE是角平分线,∴∠DAE=∠BAE.
∴∠BAE=∠AEB.
∴AB=BE.
同理AB=AF.∴AF=BE.
∴四边形ABEF是平行四边形.
∵AB=BE,∴四边形ABEF是菱形.
(2)延长BF,作DH⊥PH于H,
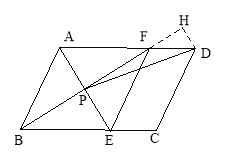
∵四边形ABEF是菱形,∠ABC=60°,AB=4,
∴AB=AF=4,∠ABF=∠AFB=30°,∠DFH=30°,
∵AD=6,AF=4,∴DF=2,
∵DH⊥PH,∠DFH=30°,
∴![]() ∴FH=
∴FH=![]() ,
,
∴DH=1,
∴在Rt△APF中,PF=AFcos30°=![]() , PH=
, PH=![]()
∴tan∠DPF=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
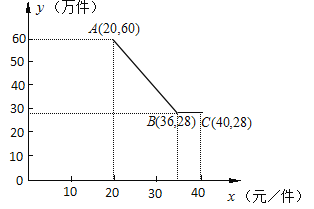
【题目】华宇公司获得授权生产某种奥运纪念品,经市场调查分析,该纪念品的销售量![]() (万件)与纪念品的价格
(万件)与纪念品的价格![]() (元/件)之间的函数图象如图所示,该公司纪念品的生产数量
(元/件)之间的函数图象如图所示,该公司纪念品的生产数量![]() (万件)与纪念品的价格
(万件)与纪念品的价格![]() (元/件)近似满足函数关系式
(元/件)近似满足函数关系式 ![]() ,若每件纪念品的价格不小于20元,且不大于40元.
,若每件纪念品的价格不小于20元,且不大于40元.
请解答下列问题:
(1)求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)当价格![]() 为何值时,使得纪念品产销平衡(生产量与销售量相等);
为何值时,使得纪念品产销平衡(生产量与销售量相等);
![]() (3)当生产量低于销售量时,政府常通过向公司补贴纪念品的价格差来提高生产量,促成新的产销平衡.若要使新的产销平衡时销售量达到46万件,政府应对该纪念品每件补贴多少元?
(3)当生产量低于销售量时,政府常通过向公司补贴纪念品的价格差来提高生产量,促成新的产销平衡.若要使新的产销平衡时销售量达到46万件,政府应对该纪念品每件补贴多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线![]() 与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
与x轴、y轴的交点分别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
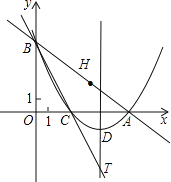
(1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;
(2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;
(3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出|QA﹣QO|的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班现要从A、B两位男生和C、D两位女生中,选派学生代表本班参加全校“中华好诗词”大赛.
(1)如果选派一位学生代表参赛,求选派到的代表是A的概率;
(2)如果选派两位学生代表参赛,求恰好选派一男一女两位同学参赛的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com