[题目]命题“同位角相等.两直线平行的逆命题是: ．题目和参考答案——青夏教育精英家教网—

【题目】命题“同位角相等，两直线平行”的逆命题是：．

【答案】两直线平行，同位角相等
【解析】解：命题：“同位角相等，两直线平行．”的题设是“同位角相等”，结论是“两直线平行”．所以它的逆命题是“两直线平行，同位角相等．”
故答案为：“两直线平行，同位角相等”．
把一个命题的题设和结论互换就得到它的逆命题．

练习册系列答案

黄冈重点中学名师编写金卷100分系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

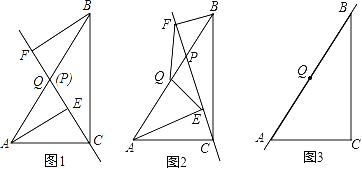
【题目】已知，点P是直角三角形ABC斜边AB上一动点（不与A，B重合），分别过A，B向直线CP作垂线，垂足分别为E，F，Q为斜边AB的中点．

（1）如图1，当点P与点Q重合时，AE与BF的位置关系是，QE与QF的数量关系式；

（2）如图2，当点P在线段AB上不与点Q重合时，试判断QE与QF的数量关系，并给予证明；

（3）如图3，当点P在线段BA（或AB）的延长线上时，此时（2）中的结论是否成立？请画出图形并给予证明．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】小华用两块不全等的等腰直角三角形的三角板摆放图形．

（1）如图①所示两个等腰直角△ABC，△DBE，两直角边交于点F，连接BF、AD，求证：BF＝AD；

（2）如果小华将两块三角板△ABC，△DBE如图②所示摆放，使D、B、C三点在一条直线上，AC、DE的延长线相交于点F，过点F作FG∥BC，交直线AE于点G，连接AD，FB，求证：FG=AC+DC；

（3）在（2）的条件下，若AG=7，DC=5，将一个45°角的顶点与点B重合，并绕点B旋转，这个角的两边分别交线段FG于P、Q两点（如图③），若PG=2，求线段FQ的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】下列四个命题：①两直线平行，内错角相等；②对顶角相等；③等腰三角形的两个底角相等；④菱形的对角线互相垂直，其中逆命题是真命题的是（　　）

A. ①②③④B. ①③④C. ①③D. ①

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】写出命题“如果两个实数相等，那么它们的绝对值相等”的逆命题：

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知抛物线y=与x轴交于A、B两点．

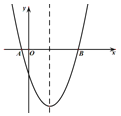
(1)点A的坐标是，点B的坐标是，抛物线的对称轴是直线；

(2)将抛物线向上平移m个单位，与x轴交于C、D两点（点C 在点D的左边）．若CD：AB=3：4，求m的值；

(3)点P是（2）中平移后的抛物线上y轴右侧部分的点，直线y=2x+b（b0）与 x、y轴分别交于点E、F．若以EF为直角边的三角形PEF与△OEF相似，直接写出点P的坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：

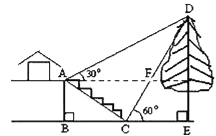
【题目】如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为2米，台阶AC的坡度为1：（即AB：BC=1：），且B、C、E三点在同一条直线上．请根据以上条件求出树DE的高度（侧倾器的高度忽略不计）．