
 同时抛掷两枚质地均匀的骰子,下列说法:(1)“两枚的点数都是3”的概率比“两枚的点数都是6”的概率大;(2)“两枚的点数相同”的概率是$\frac{1}{6}$;(3)“两枚的点数都是1”的概率最大;(4)“两枚的点数之和为奇数”与“两枚的点数之和为偶数”的概率相等.其中正确的是( )
同时抛掷两枚质地均匀的骰子,下列说法:(1)“两枚的点数都是3”的概率比“两枚的点数都是6”的概率大;(2)“两枚的点数相同”的概率是$\frac{1}{6}$;(3)“两枚的点数都是1”的概率最大;(4)“两枚的点数之和为奇数”与“两枚的点数之和为偶数”的概率相等.其中正确的是( )| A. | (1),(2) | B. | (3),(4) | C. | (1),(3) | D. | (2),(4) |
分析 由题意一共有36种等可能的结果数,然后根据概率公式一一判断即可.
解答 解:两枚的点数都是3”的概率是$\frac{1}{36}$,两枚的点数都是6的概率是$\frac{1}{36}$,故(1)错误.
共有36种等可能的结果数,其中朝上一面的点数相同的占6种,
所以朝上一面的点数相同的概率=$\frac{6}{36}$=$\frac{1}{6}$,故(2)正确.
两枚的点数都是1的概率是$\frac{1}{36}$,两枚的点数相同的概率是$\frac{1}{6}$,$\frac{1}{36}$<$\frac{1}{6}$,故(3)错误.
∵两枚的点数之和为奇数的概率是$\frac{18}{36}$=$\frac{1}{2}$,两枚的点数之和为偶数的概率=$\frac{1}{2}$,
∴两枚的点数之和为奇数与两枚的点数之和为偶数的概率相等,故(4)正确.
故选D.
点评 本题考查了列表法与树状图法:先用用列表法或树状图法列出所有可能的结果,再从中选出符合事件A或B的结果数目,求出概率.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{m}{n}$米 | B. | $\frac{5m}{n}$米 | C. | $\frac{mn}{5}$米 | D. | ($\frac{5m}{n}$-5)米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
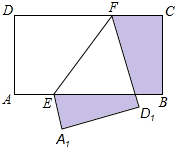 如图,在长方形ABCD中,AB=13,BC=7,点E,F分别在AB,CD上,将长方形ABCD沿EF折叠.使点A,D分别落在长方形ABCD外部的点A1,D1处,则阴影部分图形的周长为( )
如图,在长方形ABCD中,AB=13,BC=7,点E,F分别在AB,CD上,将长方形ABCD沿EF折叠.使点A,D分别落在长方形ABCD外部的点A1,D1处,则阴影部分图形的周长为( )| A. | 20 | B. | 40 | C. | 36 | D. | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com