
����Ŀ����ͼ��ʾ����ƽ���ı���ABCD�У���A=90����AB=6cm��BC=12cm����E�ɵ�A������AB�������B�����ƶ����ٶ�Ϊ1cm/s����F�ɵ�B������BC�������C�����ƶ����ٶ�Ϊ2cm/s���������E��Fͬʱ��A��B�������������EF�������˶�ʱ��Ϊts������������⣮
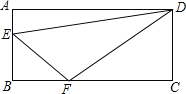
��1����tΪ ʱ����BEFΪ����ֱ�������Σ�
��2����tΪ ʱ����DFCΪ����ֱ�������Σ�
��3���Ƿ����ijһʱ�̣�ʹ��EFB�ס�FDC�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��2s����2��3s����3����t=1.5ʱ����EFB�ס�FDC��
��������
�����������1������֪������֤�ı���ABCD�Ǿ��Σ�������A=��B=��C=90��������BEFΪ����ֱ�������Σ���BE=BF�����������t��ֵ��
��2���ɣ�1����֪��C=90��������DFCΪ����ֱ�������Σ���CF=DC�����������t��ֵ��
��3������EFB�ס�FDC����BE��CF=BF��DC�������Ŀ����֪�����ɵõ�����t�ķ��̣��ⷽ�̼��ɵ�֪�Ƿ����t��ֵ��
�⣺
��1������ƽ���ı���ABCD�У���A=90����
���ı���ABCD�Ǿ��Σ�
���A=��B=��C=90����
������BEFΪ����ֱ�������Σ���BE=BF��
����E�ɵ�A������AB�������B�����ƶ����ٶ�Ϊ1cm/s����F�ɵ�B������BC�������C�����ƶ����ٶ�Ϊ2cm/s��AB=6cm��BC=12cm��
��BE=��6��t��cm��BF=2t��
��6��t=2t��
��t=2s��
�ʴ�Ϊ2s��
��2���ɣ�1����֪����DFCΪ����ֱ�������Σ���CF=DC��
��CF=2tcm��DC=6cm��
��2t=6��
��t=3s��
�ʴ�Ϊ3s��
��3������ijһʱ�̣�ʹ��EFB�ס�FDC��
�ߡ�EFB�ס�FDC��
��BE��CF=BF��DC��
��![]() ��
��
�����ã�2t2��15t+18=0��
����2t��3����t��6��=0��
��ã�t=1.5��t=6���ᣩ��
����t=1.5ʱ����EFB�ס�FDC��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������У������е�ÿ��С�����α߳���1������ABC�Ķ�����ڸ���ϣ�����������ֱ������ϵ�н���������⣺

��1��������ABC�Ƶ�A��ʱ����ת90�����A1B1C1��������ABC����ԭ��O�����ĶԳƵ���AB2C2��
��2����B1������Ϊ_________��
��C2������Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ������������ƽ�����ֱ���3a+2��a+14�������������__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=2x��˫����y=![]() �ڵ�һ���Ľ���ΪA������A��AB��x����B������ABO�Ƶ�O��ת90�㣬�õ���A��B��O�����A�������Ϊ�� ��
�ڵ�һ���Ľ���ΪA������A��AB��x����B������ABO�Ƶ�O��ת90�㣬�õ���A��B��O�����A�������Ϊ�� ��
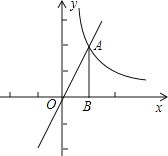
A����1��0��
B����1��0����1��0��
C����2��0����0����2��
D������2��1����2����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x�ķ���kx2+2x��1=0����������ȵ�ʵ��������k��ȡֵ��Χ�ǣ� ��
A��k����1
B��k����1
C��k�ݩ�1��k��0
D��k����1��k��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ������ƽ���ʽ������ǣ� ��
A. (a��b)(a��b) B. (��a��b)(��a��b) C. (��a+b)(a��b) D. (a��b)( ��a + b)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ҫʹƽ���ı���ABCD��Ϊ���Σ������ӵ�һ�������ǣ� ��
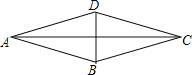
A��AB=BC
B��AC=BD
C����ABC=90��
D��AC��BD����ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������IJ�����װ��3��С������2������1���������dz���ɫ�������ͬ��
��1��������1��С���ǰ���ĸ��ʣ�
��2������1��С������ɫ��Żأ���������������1��С��������������С��ǡ����ɫ��ͬ�ĸ��ʣ���Ҫ����״ͼ���б���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A ( 5�� 3 ) �������Ϊ �� 3 �� -1�������A������������ͼ�α仯 �� ��
A .������ƽ��2����λ���ȣ�������ƽ��4����λ����
B. ������ƽ��2����λ���ȣ�������ƽ��4����λ����
C. ������ƽ��2����λ���ȣ�������ƽ��4����λ����
D. ������ƽ��2����λ���ȣ�������ƽ��4����λ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com