
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】试题分析:∵△ABD、△BCE为等边三角形,
∴AB=DB,∠ABD=∠CBE=60°,BE=BC,
∴∠ABE=∠DBC,∠PBQ=60°,
在△ABE和△DBC中,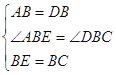 ,
,
∴△ABE≌△DBC(SAS),
∴①正确;
∵△ABE≌△DBC,
∴∠BAE=∠BDC,
∵∠BDC+∠BCD=180°﹣60°﹣60°=60°,
∴∠DMA=∠BAE+∠BCD=∠BDC+∠BCD=60°,
∴②正确;
在△ABP和△DBQ中,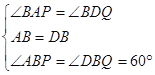 ,
,
∴△ABP≌△DBQ(ASA),∴BP=BQ,∴△BPQ为等边三角形,
∴③正确;∵∠DMA=60°,∴∠AMC=120°,∴∠AMC+∠PBQ=180°,
∴P、B、Q、M四点共圆,∵BP=BQ,∴![]() ,∴∠BMP=∠BMQ,
,∴∠BMP=∠BMQ,
即MB平分∠AMC;∴④正确;
综上所述:正确的结论有4个;
故选:D.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系xOy中,已知正比例函数y=![]() 与一次函数y=﹣x+7的图象交于点A.
与一次函数y=﹣x+7的图象交于点A.

(1)求点A的坐标;
(2)在y轴上确定点M,使得△AOM是等腰三角形,请直接写出点M的坐标;
(3)如图、设x轴上一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交y=![]() 和y=﹣x+7的图象于点B、C,连接OC,若BC=
和y=﹣x+7的图象于点B、C,连接OC,若BC=![]() OA,求△ABC的面积及点B、点C的坐标;
OA,求△ABC的面积及点B、点C的坐标;
(4)在(3)的条件下,设直线y=﹣x+7交x轴于点D,在直线BC上确定点E,使得△ADE的周长最小,请直接写出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=k1x的图象与反比例函数y=![]() 的图象的一个交点是(2,3).
的图象的一个交点是(2,3).
(1)求出这两个函数的表达式;
(2)作出两个函数的草图,利用你所作的图形,猜想并验证这两个函数图象的另一个交点的坐标;
(3)直接写出使反比例函数值大于正比例函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示1,现将点A沿x轴做如下移动:第一次点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种移动规律移动下去.第n次移动到点An,则点A2015表示的数是 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
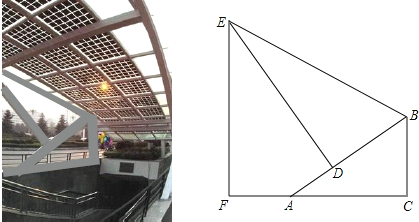
【题目】如图是某地下商业街的入口,数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E到地面的距离EF.经测量,支架的立柱BC与地面垂直,即∠BCA=90°,且BC=1.5m,点F、A、C在同一条水平线上,斜杆AB与水平线AC的夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架的边BE与AB的夹角∠EBD=60°,又测得AD=1m.请你求出该支架的边BE及顶端E到地面的距离EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
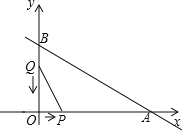
(1)设△POQ的面积为s,写出s关于t的函数关系式;当t为何值时,△POQ的面积最大,这时面积是多少
(2)当t为何值时,△POQ与△AOB相似?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com