【题目】如图：在平面直角坐标系xOy中，已知正比例函数y=与一次函数y=﹣x+7的图象交于点A．

（1）求点A的坐标；

（2）在y轴上确定点M，使得△AOM是等腰三角形，请直接写出点M的坐标；

（3）如图、设x轴上一点P（a，0），过点P作x轴的垂线（垂线位于点A的右侧），分别交y=和y=﹣x+7的图象于点B、C，连接OC，若BC=OA，求△ABC的面积及点B、点C的坐标；

（4）在（3）的条件下，设直线y=﹣x+7交x轴于点D，在直线BC上确定点E，使得△ADE的周长最小，请直接写出点E的坐标．

参考答案：

【答案】（1）（3，4）；（2）点M为（0，5）、（0，﹣5）、（0，8）、（0，）；（3）点B（9，12）、C（9，﹣2）；（4）点E坐标为（9，1）．

【解析】

试题分析：（1）联立正比例函数与一次函数解析式组成方程组，求出方程组的解得到x与y的值，确定出A坐标即可；

（2）利用勾股定理求出OA的长，根据M在y轴上，且△AOM是等腰三角形，如图1所示，分情况讨论，求出M坐标即可；

（3）设出B与C坐标，表示出BC，由已知BC与OA关系，及OA的长求出BC的长，求出a的值，如图2所示，过A作AQ垂直于BC，求出三角形ABC面积；由a的值确定出B与C坐标即可；

（4）如图3所示，作出D关于直线BC的对应点D′，连接AD′，与直线BC交于点E，此时△ADE周长最小，求出此时E坐标即可．

解：（1）联立得：，

解得：，

则点A的坐标为（3，4）；

（2）根据勾股定理得：OA==5，

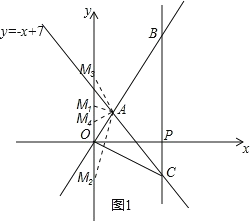
如图1所示，分四种情况考虑：

当OM1=OA=5时，M1（0，5）；

当OM2=OA=5时，M2（0，﹣5）；

当AM3=OA=5时，M3（0，8）；

当OM4=AM4时，M4（0，），

综上，点M为（0，5）、（0，﹣5）、（0，8）、（0，）；

（3）设点B（a，a），C（a，﹣a+7），

∵BC=OA=×5=14，

∴a﹣（﹣a+7）=14，

解得：a=9，

过点A作AQ⊥BC，如图2所示，

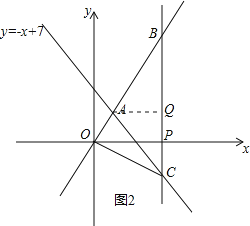
∴S△ABC=BCAQ=×14×（9﹣3）=42，

当a=9时，a=×9=12，﹣a+7=﹣9+7=﹣2，

∴点B（9，12）、C（9，﹣2）；

（4）如图3所示，作出D关于直线BC的对称点D′，连接AD′，与直线BC交于点E，连接DE，此时△ADE周长最小，

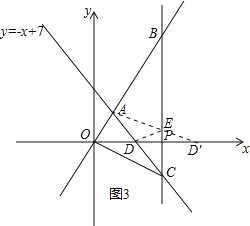
对于直线y=﹣x+7，令y=0，得到x=7，即D（7，0），

由（3）得到直线BC为直线x=9，

∴D′（11，0），

设直线AD′解析式为y=kx+b，

把A与D′坐标代入得：，

解得：，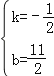

∴直线AD′解析式为y=﹣x+，

令x=9，得到y=1，

则此时点E坐标为（9，1）．

关闭