
分析 选择($\frac{1}{a-1}$-$\frac{1}{a+1}$)÷$\frac{a}{2{a}^{2}-2}$,先将括号内通分、同时将除式分母因式分解并转化为乘法,再计算括号内分式的减法,最后约分即可得.
解答 解:答案不唯一,例如:
($\frac{1}{a-1}$-$\frac{1}{a+1}$)÷$\frac{a}{2{a}^{2}-2}$
=[$\frac{a+1}{(a+1)(a-1)}$-$\frac{a-1}{(a+1)(a-1)}$]•$\frac{2(a+1)(a-1)}{a}$
=$\frac{2}{(a+1)(a-1)}$•$\frac{2(a+1)(a-1)}{a}$
=$\frac{4}{a}$,
故答案为:$\frac{1}{a-1}$,$\frac{1}{a+1}$,$\frac{a}{2{a}^{2}-2}$.
点评 本题主要考查分式的混合运算,分式的混合运算时应注意以下几点,1、注意运算顺序:分式的混合运算,先乘方,再乘除,然后加减,有括号的先算括号里面的.
2、注意化简结果:运算的结果要化成最简分式或整式.分子、分母中有公因式的要进行约分化为最简分式或整式.
3、注意运算律的应用:分式的混合运算,一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律运算,会简化运算过程.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
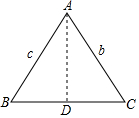 利用三角函数的定义我们可以证明某些结论,已知△ABC中,AB=c,BC=a,CA=b,则有c2=a2+b2-2abcosC,你能证明这个结论吗?(利用如图,作AD⊥BC)
利用三角函数的定义我们可以证明某些结论,已知△ABC中,AB=c,BC=a,CA=b,则有c2=a2+b2-2abcosC,你能证明这个结论吗?(利用如图,作AD⊥BC)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD中,∠ABC=∠ADC=90°,E、F分别是AC、BD的中点,∠BAC=15°,∠DAC=45°,则$\frac{EF}{CD}$的值为$\frac{\sqrt{2}}{4}$.
如图,四边形ABCD中,∠ABC=∠ADC=90°,E、F分别是AC、BD的中点,∠BAC=15°,∠DAC=45°,则$\frac{EF}{CD}$的值为$\frac{\sqrt{2}}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
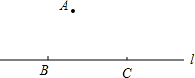 如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,则四点A、B、C、D可能组成的图形是( )
如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,则四点A、B、C、D可能组成的图形是( )| A. | 平行四边形 | B. | 梯形 | ||
| C. | 平行四边形或梯形 | D. | 平行四边形或矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$和30° | B. | $\sqrt{3}$和60° | C. | 3$\sqrt{3}$和30° | D. | 3$\sqrt{3}$和60° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
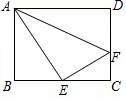 如图,在矩形ABCD中,AB=6,BC=8,点E是BC中点,点F是边CD上的任意一点,当△AEF的周长最小时,则cos∠EAF=$\frac{7\sqrt{65}}{65}$.
如图,在矩形ABCD中,AB=6,BC=8,点E是BC中点,点F是边CD上的任意一点,当△AEF的周长最小时,则cos∠EAF=$\frac{7\sqrt{65}}{65}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com