
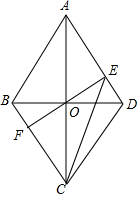
 已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.
已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.分析 (1)根据菱形的对角线互相平分可得AO=CO,对边平行可得AD∥BC,再利用两直线平行,内错角相等可得∠OAE=∠OCF,然后利用“角边角”证明△AOE和△COF全等;
(2)直接利用菱形的性质结合勾股定理求出EF的长.
解答 (1)证明:∵四边形ABCD是菱形,
∴AO=CO,AD∥BC,
∴∠OAE=∠OCF,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠OAE=∠OCF}\\{AO=CO}\\{∠AOE=∠COF}\end{array}\right.$,
∴△AOE≌△COF(ASA);
(2)解:∵∠BAD=60°,
∴∠DAO=$\frac{1}{2}$∠BAD=$\frac{1}{2}$×60°=30°,
∵∠EOD=30°,
∴∠AOE=90°-30°=60°,
∴∠AEF=180°-∠DAO-∠AOE=180°-30°-60°=90°,
∵菱形的边长为2,∠DAO=30°,
∴OD=$\frac{1}{2}$AD=$\frac{1}{2}$×2=1,
∴AO=$\sqrt{A{D}^{2}-O{D}^{2}}$=$\sqrt{3}$,
∴AE=CF=$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$,
∵菱形的边长为2,∠BAD=60°,
∴EF=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
点评 本题考查了菱形的性质、全等三角形的判定与性质、勾股定理的应用等知识,正确应用菱形的性质是解题关键.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:选择题
| 第1列 | 第2列 | 第3列 | 第4列 | … | |
| 第1行 | 1 | 2 | 9 | 10 | |
| 第2行 | 4 | 3 | 8 | 11 | |
| 第3行 | 5 | 6 | 7 | 12 | |
| 第4行 | 16 | 15 | 14 | 13 | |
| 第5行 | 17 | … | |||
| … |
| A. | 第10行第45列 | B. | 第11行第46列 | C. | 第12行第43列 | D. | 第9行第44列 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
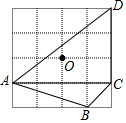 如图为4×4的网格图,A,B,C,D,O均在格点上,则点O是( )
如图为4×4的网格图,A,B,C,D,O均在格点上,则点O是( )| A. | △ACD的重心 | B. | △ABC的外心 | C. | △ACD的内心 | D. | △ABC的垂心 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
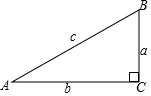 如图,试写出sinA和cosB,观察一下它们有什么关系?由你的观察试解决下面的问题:
如图,试写出sinA和cosB,观察一下它们有什么关系?由你的观察试解决下面的问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
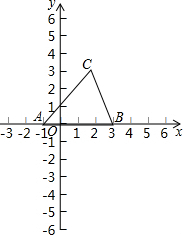 我们把一组对边平行且相等的四边形称为平行四边形,如图,在平面直角坐标系中,已知A(-1,0),B(3,0),C(2,3),你在坐标系内找一点D,使A,B,C,D形成一个平行四边形,你能找到几个这样的D点?画出所有情况的图形,并写出它们的坐标.
我们把一组对边平行且相等的四边形称为平行四边形,如图,在平面直角坐标系中,已知A(-1,0),B(3,0),C(2,3),你在坐标系内找一点D,使A,B,C,D形成一个平行四边形,你能找到几个这样的D点?画出所有情况的图形,并写出它们的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 普通间(元/人/天) | 豪华间(元/人/天) | 贵宾间(元/人/间) | |
| 三人间 | 60 | 100 | 500 |
| 双人间 | 80 | 150 | 800 |
| 单人间 | 100 | 200 | 1500 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
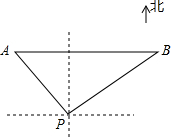 如图,小岛A位于港口P北偏西30°的方向,在小岛A的正东方向有一小岛B,小岛B位于港口P北偏东45°的方向,小岛A与港口P距离为20$\sqrt{3}$海里,则A,B两个小岛的距离为( )
如图,小岛A位于港口P北偏西30°的方向,在小岛A的正东方向有一小岛B,小岛B位于港口P北偏东45°的方向,小岛A与港口P距离为20$\sqrt{3}$海里,则A,B两个小岛的距离为( )| A. | 30海里 | B. | 30$\sqrt{3}$海里 | C. | 60海里 | D. | (30+10$\sqrt{3}$)海里 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com