练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    先化简再求值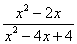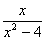：÷，其中x的值是（1）中的正整数解．


    解：原式=

    =x+2，                              

    ∵x<且x为正整数解

    ∴x=1，         

    ∴当x=1时，原式= x+2=3     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


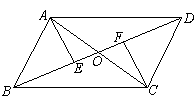
    如图，在□ABCD中，AC与BD相交于点O，AE⊥BD于E，CF⊥BD于F，那么图中的全等三角形共有……………………………………………（   ）

    A．5对          B．6对              C．7对                 D．8对

    （第8题）
     

    （第6题）
     

    （第7题）
     
     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解不等式组：         

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知a和b是有理数，若a＋b＝0，ab ≠0，则在a和b之间一定

    A．存在负整数      B．存在正整数 C．存在负分数    D．不存在正分数

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若实数a满足，则=        ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


        为了创建全国卫生城，某社区要清理一个卫生死角内的垃圾，租用甲、乙两车运送．若两车合作，各运12趟才能完成，需支付运费共4800元；若甲、乙两车单独运完此堆垃圾，则乙车所运趟数是甲车的2倍；已知乙车每趟运费比甲车少200元．

    （1）分别求出甲、乙两车每趟的运费；

     （2）若单独租用甲车运完此堆垃圾，需运多少趟；

     （3）若同时租用甲、乙两车，则甲车运x趟，乙车运y趟，才能运完此堆垃圾，其中为x，y均为正整数．

    ① 当x =10时，y =        ；

    当y =10时，x =        ；

    ② 求y与x的函数关系式．

    探究：在（3）的条件下，设总运费为w（元）．

    ①求w与x的函数关系式，直接写出w的最小值；

     ②当x≥10且y≥10时，甲车每趟的运费打7折，乙车每趟的运费打9折，直接写出w的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一元一次不等式组的解集中，整数解的个数是（　  　）

    A.4                 B.5                C.6                D.7

    查看答案和解析>>

    科目：初中数学 来源： 题型：


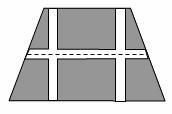
    如图，要设计一个等腰梯形的花坛，花坛上底长120米，下底长180米，上下底相距80米，在两腰中点连线（虚线）处有一条横向甬道，上下底之间有两条纵向甬道，各甬道的宽度相等．设甬道的宽为x米．

    （1）用含x的式子表示横向甬道的面积为          平方米；

    （2）当三条甬道的面积是梯形面积的八分之一时，求甬道的宽；

    （3）根据设计的要求，甬道的宽不超过6米.如果修建甬道的总费用（万元）与甬道的宽度成正比例关系，比例系数是5.7，花坛其余部分的绿化费用为每平方米0.02万元，那么当甬道的宽度为多少米时，所建花坛的总费用最少？最少费用是多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    二元一次方程3x－2y＝1的不超过10的正整数解共有(    )组．

    A. 1                    B. 2                        C. 3                        D. 4

    查看答案和解析>>

    同步练习册答案