
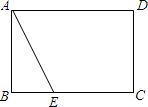
 如图所示,在矩形ABCD中,∠BAE=
如图所示,在矩形ABCD中,∠BAE=| 1 |
| 2 |
| 3 |
A、
| ||||
| B、5 | ||||
C、
| ||||
D、2
|
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
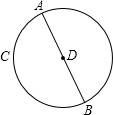 如图,在某度假旅游景区内,一艘旅游船先从A点沿⊙D的直径AB行驶到圆上的点B,然后从B点沿弧
如图,在某度假旅游景区内,一艘旅游船先从A点沿⊙D的直径AB行驶到圆上的点B,然后从B点沿弧 |
| BC |
A、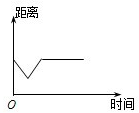 |
B、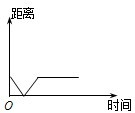 |
C、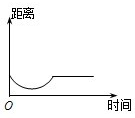 |
D、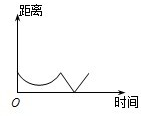 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点,连结PA、PB、PC、PD.
已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点,连结PA、PB、PC、PD.查看答案和解析>>
科目:初中数学 来源: 题型:
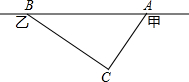 在甲村至乙村的公路有一块山地正在开发.现有一C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?请通过计算进行说明.
在甲村至乙村的公路有一块山地正在开发.现有一C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?请通过计算进行说明.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com