Question

如图，已知正方形ABCD，点E是边AB的中点，点O是线段AE上的一个动点（不与A、E重合），以O为圆心，OB为半径的圆与边AD相交于点M，过点M作⊙O的切线交DC于点N，连接OM、ON、BM、BN．记△MNO、△AOM、△DMN的面积分别为S₁、S₂、S₃，则下列结论不一定成立的是（　　）

A．S₁＞S₂+S₃       B．△AOM∽△DMN   C．∠MBN=45°    D．MN=AM+CN

　

Answer 1

A【考点】切线的性质；正方形的性质；相似三角形的判定与性质．

【分析】（1）如图作MP∥AO交ON于点P，当AM=MD时，求得S₁=S₂+S₃，

（2）利用MN是⊙O的切线，四边形ABCD为正方形，求得△AOM∽△DMN．

（3）作BP⊥MN于点P，利用Rt△MAB≌Rt△MPB和Rt△BPN≌Rt△BCN来证明C，D成立．

【解答】解：（1）如图，作MP∥AO交ON于点P，

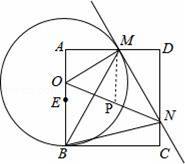
∵点O是线段AE上的一个动点，当AM=MD时，

S_梯形ONDA=（OA+DN）•AD

S_△MNO=S_△MOP+S_△MPN=MP•AM+MP•MD=MP•AD，

∵（OA+DN）=MP，

∴S_△MNO=S_梯形ONDA，

∴S₁=S₂+S₃，

∴不一定有S₁＞S₂+S₃，

（2）∵MN是⊙O的切线，

∴OM⊥MN，

又∵四边形ABCD为正方形，

∴∠A=∠D=90°，∠AMO+∠DMN=90°，∠AMO+∠AOM=90°，

∴∠AOM=∠DMN，

在△AMO和△DMN中，

，

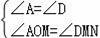
∴△AOM∽△DMN．

故B成立；

（3）如图，作BP⊥MN于点P，

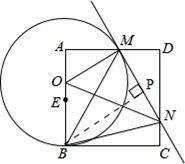
∵MN，BC是⊙O的切线，

∴∠PMB=∠MOB，∠CBM=∠MOB，

∵AD∥BC，

∴∠CBM=∠AMB，

∴∠AMB=∠PMB，

在Rt△MAB和Rt△MPB中，

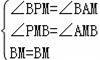
∴Rt△MAB≌Rt△MPB（AAS）

∴AM=MP，∠ABM=∠MBP，BP=AB=BC，

在Rt△BPN和Rt△BCN中，

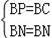
∴Rt△BPN≌Rt△BCN（HL）

∴PN=CN，∠PBN=∠CBN，

∴∠MBN=∠MBP+∠PBN，

MN=MP+PN=AM+CN．

故C，D成立，

综上所述，A不一定成立，

故选：A．

【点评】本题主要考查了圆的切线及全等三角形的判定和性质，关键是作出辅助线利用三角形全等证明．