
����Ŀ����ͼ��������y=��x2+bx+c����A����1��0����C��0��4�����㣬��x�ύ����һ��B��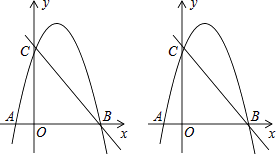
��1���������ߵĽ���ʽ��
��2����P�ڵ�һ�����������ϣ�P��ĺ�����Ϊt������P��x�������߽�ֱ��BC�ڵ�Q�����߶�PQ�ij�Ϊm����m��t֮��ĺ�����ϵʽ�����m�����ֵ��
��3���ڣ�2���������£���������һ��D��������Ϊm�����ֵ������BD�����������Ƿ���ڵ�E�������A��B��C�غϣ�ʹ�á�DBE=45�㣿�������ڣ���˵�����ɣ�����������E������꣮
���𰸡�
��1��
�⣺������y=��x2+bx+c����A����1��0����C��0��4�����㣬
�� ![]() ���
��� ![]()
�������ߵĽ���ʽy=��x2+3x+4
��2��
�⣺�x2+3x+4=0��
���x1=��1��x2=4��
��B��4��0��
��ֱ��BC�Ľ���ʽΪy=kx+a
�� ![]() ���
��� ![]() ��
��
��ֱ��BC�Ľ���ʽΪy=��x+4
��P���������t����t2+3t+4������Q���������t����t+4��
��m=����t2+3t+4��������t+4��=����t��2��2+4
������m=����t��2��2+4��
�൱t=2ʱ��m�����ֵΪ4
��3��
�⣺����
��������һ��D��������Ϊm�����ֵ4��
�ੁx2+3x+4=4�����x1=0���ᣩ��x2=3
��D��3��4����CD=3
��C��0��4����
��CD��x�ᣬ
��OC=OB=4��
���BOCΪֱ�������Σ�
����D��DH��BC��H������E��EF��x�ڵ�F���ڡ�CDB�У�CD=3����DCB=45��
��CH=DH= ![]() ��
��
��CB=4 ![]() ����BH=CB��CH=
����BH=CB��CH= ![]()
�ߡ�DBE=��CBO=45��
���DBE����CBE=��CBO����CBE��
����DBC=��EBF
��tan��DBC= ![]() =
= ![]() =
= ![]()
��EF=3a��BF=5a
��OF=5a��4
��F��4��5a��0����E��4��5a��3a��
�ߵ�E����������
��3a=����4��5a��2+3��4��5a��+4
���a1=0 a2= ![]()
��E���� ![]() ��
�� ![]() ����
����

����������1���ѵ�A��B��������������߽���ʽ�������b��c�ķ��������b��c��ֵ���ɵõ������߽���ʽ����y=0�������x��һԪ���η��̼��ɵõ���C�����ꣻ��2�����������ߵĽ���ʽy=��x2+3x+4����y=0��õ�B������Ϊ��4.0������ֱ��BC�Ľ���ʽΪy=kx+a�ѵ�B��C���������ֱ��BC�Ľ���ʽΪy=kx+a�������k��a�ķ��������k��a��ֵ������ֱ��BC�Ľ���ʽΪy=��x+4����P�������Ϊ��t����t2+3t+4������Q�������Ϊ��t����t+4��������m=����t2+3t+4��������t+4����������m=����t��2��2+4�����ݹ���m��t�Ķ��κ���������ã���3������m�����ֵ��4������y=��x2+3x+4�������D������꣨3��4������D����DH��BC����E����EF��x�ᣬ��OC=OB=4�á�DCBΪ����ֱ�������Σ��Ӷ��ó���CDHΪ����ֱ�������Σ�ͨ������ֱ�����������CN��BH��ֵ��Ȼ������������������EF��BF�Ĺ�ϵ�����E������꣬Ȼ�����y=��x2+3x+4������ã�
�����㾫����������Ҫ�����˶��κ��������ʵ����֪ʶ�㣬��Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮


 ��һ������ĩ�ٷֳ�̾�ϵ�д�
��һ������ĩ�ٷֳ�̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ƻ�����9��Ԫ�ӳ��ҹ���50̨���ӻ�![]() ��֪�ó����������ֲ�ͬ�ͺŵĵ��ӻ��������۷ֱ�Ϊ������ÿ̨1500Ԫ������ÿ̨2100Ԫ������ÿ̨2500Ԫ��
��֪�ó����������ֲ�ͬ�ͺŵĵ��ӻ��������۷ֱ�Ϊ������ÿ̨1500Ԫ������ÿ̨2100Ԫ������ÿ̨2500Ԫ��
![]() ���̳�ͬʱ�����������ֲ�ͬ�ͺŵ��ӻ���50̨����ȥ9��Ԫ�����о�һ���̳��Ľ���������
���̳�ͬʱ�����������ֲ�ͬ�ͺŵ��ӻ���50̨����ȥ9��Ԫ�����о�һ���̳��Ľ���������
![]() ���̳�����һ̨���ֵ��ӻ��ɻ���150Ԫ������һ̨���ֵ��ӻ��ɻ���200Ԫ������һ̨���ֵ��ӻ��ɻ���250Ԫ
���̳�����һ̨���ֵ��ӻ��ɻ���150Ԫ������һ̨���ֵ��ӻ��ɻ���200Ԫ������һ̨���ֵ��ӻ��ɻ���250Ԫ![]() ��ͬʱ�������ֲ�ͬ�ͺŵ��ӻ��ķ����У�Ϊʹ����ʱ������࣬��ѡ�����ֽ���������
��ͬʱ�������ֲ�ͬ�ͺŵ��ӻ��ķ����У�Ϊʹ����ʱ������࣬��ѡ�����ֽ���������
![]() ���̳�����9��Ԫͬʱ�������ֲ�ͬ�ĵ��ӻ�50̨��������ƽ���������
���̳�����9��Ԫͬʱ�������ֲ�ͬ�ĵ��ӻ�50̨��������ƽ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��ı���ABCD�У�BC��AD����A=90�㣬��P��A�������������AB��BC��CD�˶�������Dʱֹͣ����֪��PAD�����s���P�˶���·��x�ĺ���ͼ����ͼ����ʾ�����P�ӿ�ʼ��ֹͣ�˶�����·��Ϊ�� ��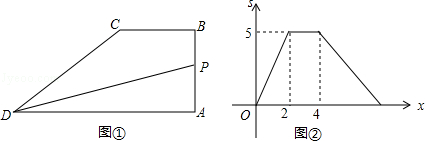
A.4
B.2+ ![]()
C.5
D.4+ ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������Ľ����ɰ�Բ�ͳ����ι��ɣ������εij�BCΪ8m����ABΪ1m������������˫����ʻ�ij���(����2������)��������һ�����˿�����4m����2.3m�����������˿����ܷ�ͨ����������˵������.
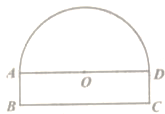
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����OEFG�Ķ���E������Ϊ��4��0��������G������Ϊ��0��2����������OEFG�Ƶ�O��ʱ����ת��ʹ��F����y��ĵ�N�����õ�����OMNP��OM��GF���ڵ�A��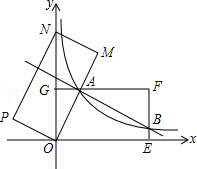
��1����ͼ����A�ķ����������Ľ���ʽ��
��2���裨2���еķ���������ͼ��EF�ڵ�B��ֱ��д��ֱ��AB�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��Rt��ABC�У���ABC=90�㣬��D��BC�ߵ��е㣬�ֱ���B��CΪԲ�ģ������߶�BC����һ��ij�Ϊ�뾶������������ֱ��BC�Ϸ��Ľ���ΪP��ֱ��PD��AC�ڵ�E������BE�������н��ۣ���ED��BC���ڡ�A=��EBA����EBƽ�֡�AED����ED= ![]() AB�У�һ����ȷ���ǣ� ��
AB�У�һ����ȷ���ǣ� �� 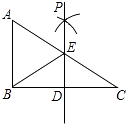
A.�٢ڢ�
B.�٢ڢ�
C.�٢ۢ�
D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ�� ![]() �£�a+2��
�£�a+2�� ![]() ��������x2��2
��������x2��2 ![]() x+a=0����������ȵ�ʵ��������aΪ�Ǹ�������
x+a=0����������ȵ�ʵ��������aΪ�Ǹ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
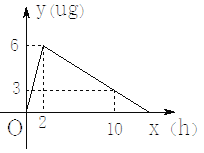
����Ŀ��ijҽҩ�о���������һ����ҩ����ʵ��ҩЧʱ���֣�������˰���������ã���ô����ҩ��2hʱѪҺ�к�ҩ����ߣ���ÿ����6ug��������˥����10hʱѪҺ�к�ҩ��ÿ����3ug��ÿ����ѪҺ�к�ҩ��y��ug����ʱ��x��h���ı仯��ͼ��ʾ�������˰��涨������ҩ��.
��1���ֱ����x��2��x>2ʱ��y��x֮��ĺ�����ϵʽ��
��2�����ÿ����ѪҺ��ҩ��Ϊ4ug��4ug����ʱ�����Ƽ���ʱ����Ч�ģ���ô�����Чʱ���Ƕ��ÿ�����ٳԼ���ҩ��Ч��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ĵ��Ű����������ijУѧ������ȫУ1900��ѧ������������ϵ�Ű��������Ϊ�˽��������ѧ������������˲���ѧ���ľ������õõ������ݻ���������ͳ��ͼ�ٺ�ͼ�ڣ�����������Ϣ��������������⣺

��1�����ν���������������ѧ������Ϊ ��ͼ����m��ֵ�� ��
��2���ε����ȡ���������ݵ�ƽ��������������λ����
��3�������������ݣ����Ƹ�У���λ�����Ϊ10Ԫ��ѧ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com