
【题目】如图,在四边形ABCD中,BA=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
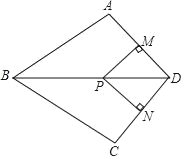
(1)求证:点A与C关于直线BD对称.
(2)若∠ADC=90°,求证四边形MPND为正方形.
【答案】见解析
【解析】
(1)首先根据角平分线的定义求出∠ABD=∠CBD,然后在△ABD和△CBD中,根据SAS证明两个三角形全等,进而得到∠ADB=∠CDB,AD=CD,根据等腰三角形的性质可得BD垂直平分AC,进而可得点A与C关于直线BD对称;
(2)首先证明四边形PMDN是矩形,再根据角平分线上的点到角两边的距离相等可得PM=PN,进而可得四边形MPND为正方形.
证明:(1)连接AC,
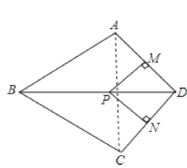
∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中
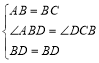 ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,DA=DC,
∴BD垂直平分AC,
∴点A与C关于直线BD对称;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形PMDN是矩形,
∵∠ADB=∠CDB,
∴BD平分∠ADC,
∵PM⊥AD,PN⊥CD,
∴PM=PN,
∴四边形MPND为正方形


科目:初中数学 来源: 题型:
【题目】某校准备在国庆节期间组织学生到泰山进行研学旅行,已知老师与学生一共25人参加此次研学旅行,购买门票共花费1700元,门票费用如表格所示,求参加研学旅行的老师和学生各有多少人?设老师有x人,学生有y人,则可列方程组为( )
景点 | 票价 | 开放时间 |
泰山门票 | 旺季:125元/人 淡季:100元/人 | 全天 |
说明:(1)旺季时间(2月~11月),淡季时间(12月-次年1月); (2)老年人(60岁~70岁)、学生、儿童(1.2米~1.4米)享受5折优惠; (3)教师、省部级劳模、英模、道德模范享受8折优惠; (4)现役军人、伤残军人、70岁以上老年人、残疾人,凭本人有效证件免费进山; (5)享受优惠的游客请出示本人有效证件。 | ||
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的关系是___;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径.如图,若这个输水管道有水部分的水面宽AB=16cm,水最深的地方的高度为4cm,求这个圆形截面的半径.
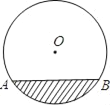
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察理解,并解决问题.
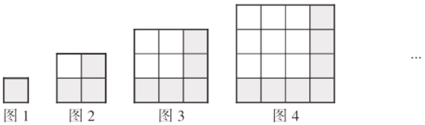
问题情境:如图所示,用一些相同的小正方形,拼在一起,排成如下的一些大正方形:
问题解决:(1)完成下表:
图序号 | 1 | 2 | 3 | 4 | … |
|
每一行小正方形的个数 | 1 | 2 | 3 | ______ | … | ______ |
阴影小正方形的个数 | 1 | 3 | 5 | ______ | … | ______ |
(2)根据图形规律推测:![]() ______(用含
______(用含![]() 的代数式表示)
的代数式表示)
(3)像(1),(2)这样,根据某类事物的部分对象具有的某种性质,推出这类事物的所有对象具有的这种性质的推理,叫做归纳推理.对于科学的发现,归纳推理是十分有用的,通过观察、实验,对有限个对象的性质作归纳整理,提出对某类事物带有规律性的猜测,是科学研究的基本方法.请观察下列等式的规律:第一个等式:![]() ;第二个等式:
;第二个等式:![]() ;第三个等式:
;第三个等式:![]() ;…猜想并直接写出第
;…猜想并直接写出第![]() 个等式.(用含
个等式.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用方程解答下列问题
(1)一件工作,甲单独做20小时完成,乙单独做12小时完成,现在先由甲单独做4小时,余下的由甲乙一起完成余下的部分需要几小时完成?
(2)王强参加了一场3000米的赛跑,他以6米/秒的速度跑了一段路程,又以4米/秒的速度跑完了其余的路程,一共花了10分钟,王强以6米秒的速度跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.
(1)①∠BCE与∠CDF的大小关系是_______________;
②证明:GF⊥BF;
(2)探究G落在边DC的什么位置时,BF=BC,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 城气象台测得台风中心在
城气象台测得台风中心在![]() 城正西方向
城正西方向![]() 的
的![]() 处,以每小时
处,以每小时![]() 的速度向南偏东
的速度向南偏东![]() 的
的![]() 方向移动,距台风中心
方向移动,距台风中心![]() 的范围内是受台风影响的区域.
的范围内是受台风影响的区域.

(1)求![]() 城与台风中心之间的最小距离;(2)求
城与台风中心之间的最小距离;(2)求![]() 城受台风影响的时间有多长?
城受台风影响的时间有多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com