
【题目】如图,平行四边形ABCD中,D点在抛物线y= ![]() x2+bx+c上,且OB=OC,AB=5,tan∠ACB=
x2+bx+c上,且OB=OC,AB=5,tan∠ACB= ![]() ,M是抛物线与y轴的交点.
,M是抛物线与y轴的交点.
(1)求直线AC和抛物线的解析式;
(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动.问:当P运动到何处时,△APQ是直角三角形?
(3)在(2)中当P运动到某处时,四边形PDCQ的面积最小,求此时△CMQ的面积.
【答案】
(1)
解:如图1,∵tan∠ACB= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴设AO=3x,CO=4x,∵OB=OC,
∴BO=4x,
∴AB2=AO2+BO2,
则25=25x2,
解得:x=1(负数舍去),
∴AO=3,BO=CO=4,
∴A(0,3),B(﹣4,0),C(4,0),
∴设直线AC的解析式为:y=kx+d,
则 ![]() ,
,
解得:  ,
,
故直线AC的解析式为:y=﹣ ![]() x+3;
x+3;
∵四边形ABCD是平行四边形,
∴BC=AD=8,
∴D(8,3),
∵B,D点都在抛物线y= ![]() x2+bx+c上,
x2+bx+c上,
∴  ,
,
解得:  ,
,
故此抛物线解析式为:y= ![]() x2﹣
x2﹣ ![]() x﹣3
x﹣3

(2)
解:①如图2,∵OA=3,OB=4,

∴AC=5.
设点P运动了t秒时,PQ⊥AC,此时AP=t,CQ=t,AQ=5﹣t,
∵PQ⊥AC,
∴∠AQP=∠AOC=90°,∠PAQ=∠ACO,
∴△APQ∽△CAO,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:t= ![]() .
.
②如图3,

设点P运动了t秒时,当QP⊥AD,此时AP=t,CQ=t,AQ=5﹣t,
∵QP⊥AD,
∴∠APQ=∠AOC=90°,∠PAQ=∠ACO,
∴△AQP∽△CAO,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:t= ![]() .
.
即当点P运动到距离A点 ![]() 或
或 ![]() 个单位长度处,△APQ是直角三角形
个单位长度处,△APQ是直角三角形
(3)
解:如图4,∵S四边形PDCQ+S△APQ=S△ACD,且S△ACD= ![]() ×8×3=12,
×8×3=12,
∴当△APQ的面积最大时,四边形PDCQ的面积最小,
当动点P运动t秒时,AP=t,CQ=t,AQ=5﹣t,
设△APQ底边AP上的高为h,作QH⊥AD于点H,
由△AQH∽△CAO可得: ![]() =
= ![]() ,
,
解得:h= ![]() (5﹣t),
(5﹣t),
∴S△APQ= ![]() t×
t× ![]() (5﹣t)=
(5﹣t)= ![]() (﹣t2+5t)=﹣
(﹣t2+5t)=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
∴当t= ![]() 时,S△APQ达到最大值
时,S△APQ达到最大值 ![]() ,此时S四边形PDCQ=12﹣
,此时S四边形PDCQ=12﹣ ![]() =
= ![]() ,
,
故当点P运动到距离点A, ![]() 个单位处时,四边形PDCQ面积最小,
个单位处时,四边形PDCQ面积最小,
则AQ=QC= ![]() ,
,
故△CMQ的面积为: ![]() S△AMC=
S△AMC= ![]() ×
× ![]() ×4×6=6.
×4×6=6.

【解析】(1)首先利用锐角三角函数关系得出A,C点坐标,再求出一次函数解析式,根据平行四边形的性性质求出点D坐标,利用待定系数法可求出b、c的值,继而得出二次函数表达式;(2)设点P运动了t秒时,PQ⊥AC,此时AP=t,CQ=t,AQ=5﹣t,再由△APQ∽△CAO或△AQP∽△CAO,利用对应边成比例可求出t的值,继而确定点P的位置;(3)只需使△APQ的面积最大,就能满足四边形PDCQ的面积最小,设△APQ底边AP上的高为h,作QH⊥AD于点H,由△AQH∽△CAO,利用对应边成比例得出h的表达式,继而表示出△APQ的面积表达式,即可得出四边形PDCQ的最小值,也可确定点P的位置,进而得出Q的位置,进而得出△CMQ的面积.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=45°,∠C=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,在AG上取点F,连接DF.延长DA至E,使AE=AF,连接EG,DG,且GE=DF.
(1)若AB=2 ![]() ,求BC的长;
,求BC的长;
(2)如图1,当点G在AC上时,求证:BD= ![]() CG;
CG;
(3)如图2,当点G在AC的垂直平分线上时,直接写出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE= ![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是(填序号)
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是(填序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线 ![]() 交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.
交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.
(1)求抛物线的解析式及顶点D的坐标.
(2)如图1,当0≤t≤4时,设△PAD的面积为S,求出S与t之间的函数关系式;S是否有最小值?如果有,求出S的最小值和此时t的值.
(3)如图2,当点P运动到使∠PDA=90°时,Rt△ADP与Rt△AOC是否相似?若相似,求出点P的坐标;若不相似,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,D点在抛物线y= ![]() x2+bx+c上,且OB=OC,AB=5,tan∠ACB=
x2+bx+c上,且OB=OC,AB=5,tan∠ACB= ![]() ,M是抛物线与y轴的交点.
,M是抛物线与y轴的交点.
(1)求直线AC和抛物线的解析式;
(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动.问:当P运动到何处时,△APQ是直角三角形?
(3)在(2)中当P运动到某处时,四边形PDCQ的面积最小,求此时△CMQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论不正确的是( )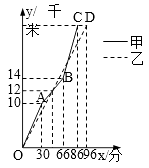
A.甲先到达终点
B.前30分钟,甲在乙的前面
C.第48分钟时,两人第一次相遇
D.这次比赛的全程是28千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)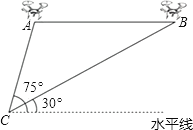
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com