
 将抛物线在第四象限之间的部分图象记为图象G,如果直线y=k(x+1)-4与图象G有公共点,请结合图象,求直线y=k(x+1)-4与y轴交点的纵坐标t的取值范围.
将抛物线在第四象限之间的部分图象记为图象G,如果直线y=k(x+1)-4与图象G有公共点,请结合图象,求直线y=k(x+1)-4与y轴交点的纵坐标t的取值范围. 分析 待定系数法求出抛物线解析式,配方后可得抛物线的顶点坐标,当直线经过抛物线顶点时t取得最小值,当直线经过抛物线与y轴的交点(0,-3)时t取得最大值,继而得出答案.
解答 解:由图象可知抛物线与x轴的交点为(-1,0)、(3,0),
设抛物线解析式为y=a(x+1)(x-3),
将(0,-3)代入,得:-3=-3a,
解得:a=1,
∴抛物线解析式为y=(x+1)(x-3)=x2-2x-3=(x-1)2-4,
∴抛物线的顶点坐标为(1,-4),
当直线y=k(x+1)-4经过顶点(1,-4)时,-4=k(1+1)-4,
解得:k=0,
此时直线与y轴交点的纵坐标为-4;
∵抛物线与y轴交点的纵坐标为-3,
∴-4≤t<-3.
点评 本题主要考查二次函数图象上点的坐标特征和待定系数求函数解析式,理解题意确定直线与抛物线相交时的临界情况是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
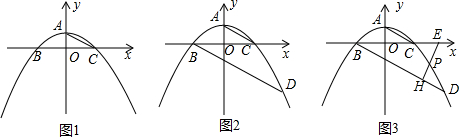
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知△ABC中,AC=6cm,BC=8cm,AB=10cm,CD为AB边上的高.动点P从点A出发,沿着△ABC的三条边逆时针走一圈回到A点,速度为2cm/s,设运动时间为ts.
已知△ABC中,AC=6cm,BC=8cm,AB=10cm,CD为AB边上的高.动点P从点A出发,沿着△ABC的三条边逆时针走一圈回到A点,速度为2cm/s,设运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 单项式a的系数是0 | |
| B. | 单项式-$\frac{3xy}{5}$的系数和次数分别是-3和2 | |
| C. | 单项式-3πxy2z3的系数和次数分别是-3π和6 | |
| D. | 3mn与4nm不是同类项 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
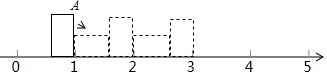
| 翻动次数 | A点在数轴上对应的数字 |
| 1 | 1+$\frac{3}{4}$ |
| 2 | 1+$\frac{3}{4}$+0 |
| 3 | |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com