
 如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB绕点O按顺时针方向旋转120°得到△OA′B′,则点A′的坐标是( )
如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB绕点O按顺时针方向旋转120°得到△OA′B′,则点A′的坐标是( )| A. | (2,-2$\sqrt{2}$) | B. | (2,-2$\sqrt{3}$) | C. | (2$\sqrt{2}$,2) | D. | (2$\sqrt{3}$,2) |
分析 在直角△OAB中利用直角三角形的性质求得∠AOB的度数,作A'C⊥OB于点C,在直角△OA'C中利用三角函数求得A'C和OC的长,则C'的坐标即可求得.
解答 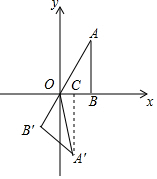 解:在直角△OAB中,∠AOB=90°-∠A=90°-30°=60°,
解:在直角△OAB中,∠AOB=90°-∠A=90°-30°=60°,
∠AOA'=120°,
则∠BOA'=∠AOA'-∠AOB=120°-60°=60°,
作A'C⊥OB于点C.
在直角△OA'C中,OA'=OA=4,
则A'C=OA'•sin∠BOA'=4sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,OC=OA'•cos∠BOA'=4cos60°=4×$\frac{1}{2}$=2,
则A'的坐标是(2,-2$\sqrt{3}$).
故选B.
点评 本题考查了坐标与图形的变化,求坐标的问题常用的思路是转化为求线段的长的问题.


科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD内有两点E、F满足AE=1,EF=FC=3,AE⊥EF,CF⊥EF,则正方形ABCD的面积为( )
如图,正方形ABCD内有两点E、F满足AE=1,EF=FC=3,AE⊥EF,CF⊥EF,则正方形ABCD的面积为( )| A. | $\frac{25}{2}$ | B. | 10$\sqrt{2}$ | C. | 20 | D. | 20$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
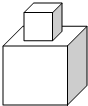 如图所示的某种玩具是由两个正方体用胶水黏合而成的,它们的棱长分别为1dm和2dm,为了美观,现要在其表面喷涂油漆,如果喷涂1dm2需用油漆4g,那么喷涂这个玩具共需油漆112g.
如图所示的某种玩具是由两个正方体用胶水黏合而成的,它们的棱长分别为1dm和2dm,为了美观,现要在其表面喷涂油漆,如果喷涂1dm2需用油漆4g,那么喷涂这个玩具共需油漆112g.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com