【题目】如图，在△ABC中，∠ACB=120°，BC=2AC．

（1）利用尺规作等腰△DBC，使点D、A在直线BC的同侧，且DB=BC，∠DBC=∠ACB（保留作图痕迹，不写画法）；

（2）设（1）中所作的△DBC的边DC交AB于E点，求证：DE=3CE．

参考答案：

【答案】（1）作图见解析；（2）证明见解析.

【解析】试题分析：（1）按照题意画出相应的图形，如图所示；

（2）利用等腰三角形BCD的性质、△DBC的内角和定理和图形中的角与角间的数量关系来求∠ACE的度数；过点B作BM⊥DC于点M．由全等三角形△BME与△ACE的对应边相等推知ME=CE=MC．然后根据等腰三角形“三合一”的性质证得DM=MC，最后由等量代换证得结论．

试题解析：（1）如图所示，根据题意画出图形；

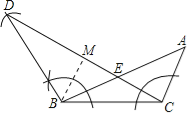
（2）∵BD=BC（已知），

∴∠D=∠BCD（等边对等角）．

又∵∠DBC=120°，∠D+∠BCD+∠DBC=180°（三角形内角和定理），

∴∠D=∠BCD=30°．

∵∠ACB=120°，∠ACB=∠ACE+∠BCD，

∴∠ACE=90°，

过点B作BM⊥DC于点M，

在Rt△BMC中，由∠BCD=30°，得BM=BC，

∵BC=2AC，

∴AC=BC，

∴BM=AC，

在△BME与△ACE中，

∵，

∴△BME≌△ACE（AAS），

∴ME=CE=MC．

∵BD=BC，BM⊥DC，

∴DM=MC，

∴ME=CE=DM，

∴DE=3CE．

关闭