
【题目】如图,已知正方形ABCD,点E在CB的延长线上,联结AE、DE,DE与边AB交于点F,FG∥BE且与AE交于点G. 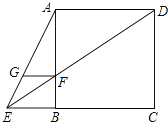
(1)求证:GF=BF.
(2)在BC边上取点M,使得BM=BE,联结AM交DE于点O.求证:FOED=ODEF.
【答案】
(1)证明:∵四边形ABCD是正方形,
∴AD∥BC,AB∥CD,AD=CD,
∵GF∥BE,
∴GF∥BC,
∴GF∥AD,
∴ ![]() ,
,
∵AB∥CD,
∴ ![]() ,
,
∵AD=CD,
∴GF=BF;
(2)证明:延长GF交AM于H,
∵GF∥BC,
∴FH∥BC,
∴ ![]() ,
,
∴ ![]() ,
,
∵BM=BE,
∴GF=FH,
∵GF∥AD,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴FOED=ODEF.
【解析】(1)根据已知条件可得到GF∥AD,则有 ![]() ,由BF∥CD可得到
,由BF∥CD可得到 ![]() ,又因为AD=CD,可得到GF=FB;(2)延长GF交AM于H,根据平行线分线段成比例定理得到
,又因为AD=CD,可得到GF=FB;(2)延长GF交AM于H,根据平行线分线段成比例定理得到 ![]() ,由于BM=BE,得到GF=FH,由GF∥AD,得到
,由于BM=BE,得到GF=FH,由GF∥AD,得到 ![]() ,等量代换得到
,等量代换得到 ![]() ,即
,即 ![]() ,于是得到结论.
,于是得到结论.
【考点精析】本题主要考查了正方形的性质和相似三角形的判定与性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】已知正方形ABC1D1的边长为1,延长C1D1到A1 , 以A1C1为边向右作正方形A1C1C2D2 , 延长C2D2到A2 , 以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推….若A1C1=2,且点A,D2 , D3 , …,D10都在同一直线上,则正方形A9C9C10D10的边长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本中有一道作业题: 有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.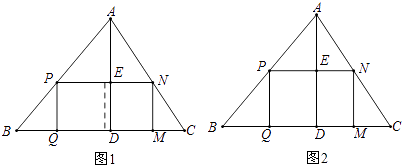
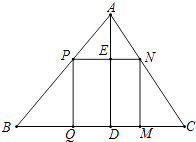
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路. 
(1)求改直的公路AB的长;
(2)问公路改直后比原来缩短了多少千米?(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AC与BD交于O点,DO:BO=1:2,点E在CB的延长线上,如果S△AOD:S△ABE=1:3,那么BC:BE= . 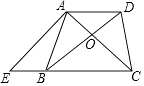
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,点D在边BC上,∠DAB=∠B,点E在边AC上,满足AECD=ADCE. 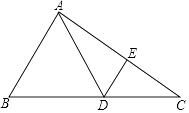
(1)求证:DE∥AB;
(2)如果点F是DE延长线上一点,且BD是DF和AB的比例中项,联结AF.求证:DF=AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AB=5,tanA= ![]() ,将△ABC沿直线l翻折,恰好使点A与点B重合,直线l分别交边AB、AC于点D、E;
,将△ABC沿直线l翻折,恰好使点A与点B重合,直线l分别交边AB、AC于点D、E; 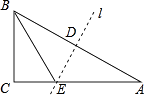
(1)求△ABC的面积;
(2)求sin∠CBE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE. 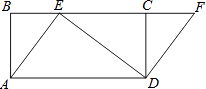
(1)求证:四边形AEFD是平行四边形;
(2)若DF=3,DE=4,AD=5,求CD的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com