
【题目】如图,矩形ABCD的四个顶点正好落在四条平行线上,并且从上到下每两条平行线间的距离都是1,如果AB:BC=3:4,那么AB的长是 . 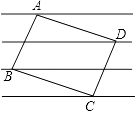
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】设函数y=(x﹣1)[(k﹣1)x+(k﹣3)](k是常数). 
(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时的函数的图象;
(2)根据图象,写出你发现的一条结论;
(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到的函数y3的图象,求函数y3的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;
综合运用:
(3)在(2)问条件下,HF∥GE,如图3所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E在CB的延长线上,联结AE、DE,DE与边AB交于点F,FG∥BE且与AE交于点G. 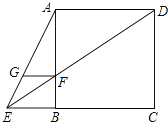
(1)求证:GF=BF.
(2)在BC边上取点M,使得BM=BE,联结AM交DE于点O.求证:FOED=ODEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知梯形ABCD中,AD∥BC,AB=4,AD=3,AB⊥AC,AC平分∠DCB,过点DE∥AB,分别交AC、BC于F、E,设 ![]() =
= ![]() ,
, ![]() =
= ![]() .求:
.求: 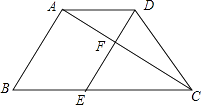
(1)向量 ![]() (用向量
(用向量 ![]() 、
、 ![]() 表示);
表示);
(2)tanB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平行四边形ABCD中,点E是CD上一点,且DE=2,CE=3,射线AE与射线BC相交于点F; 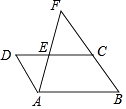
(1)求 ![]() 的值;
的值;
(2)如果 ![]() =
= ![]() ,
, ![]() =
= ![]() ,求向量
,求向量 ![]() ;(用向量
;(用向量 ![]() 、
、 ![]() 表示)
表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Word文本中的图形,在图形格式中大小菜单下显示有图形的绝对高度和绝对宽度,同一个图形随其放置方向的变化,所显示的绝对高度和绝对宽度也随之变化.如图①、②、③是同一个三角形以三条不同的边水平放置时,它们所显示的绝对高度和绝对宽度如下表,现有△ABC,已知AB=AC,当它以底边BC水平放置时(如图④),它所显示的绝对高度和绝对宽度如下表,那么当△ABC以腰AB水平放置时(如图⑤),它所显示的绝对高度和绝对宽度分别是( ) 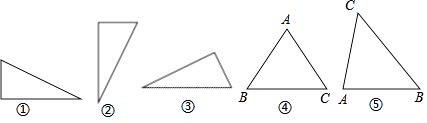
图形 | 图① | 图② | 图③ | 图④ | 图⑤ |
绝对高度 | 1.50 | 2.00 | 1.20 | 2.40 | ? |
绝对宽度 | 2.00 | 1.50 | 2.50 | 3.60 | ? |
A.3.60和2.40
B.2.56和3.00
C.2.56和2.88
D.2.88和3.00
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动:拼图中的数学 数学活动课上,老师提出如下问题:
用5个边长为1的小正方形组合一个图形(相互之间不能重叠),然后将组合后的图形剪拼成一个大的正方形.
合作交流:“实践”小组:我们组合成的图形如图(1)所示,剪拼成大的正形的过程如图(2),图(3)所示.“兴趣”小组:我们组合成的图形如图(4)所示,但我们未能将其剪拼成大的正方形.
任务:请你帮助“兴趣”小组的同学,在图(4)中画出剪拼线,在图(5)中画出剪拼后的正方形.要求:剪拼线用虚线表示,剪拼后的大正方形用实线表示.
应用迁移:如图(6),∠A=∠B=∠C=∠D=∠F=90°,AB=AF=2,EF=ED=1.
请你将该图进行分割,使得分割后的各部分恰好能拼成一个正方形,请你在图(5)中画出拼图示意图(拼图的各部分不能互相重叠,不能留有空隙,不要求进行说理或证明)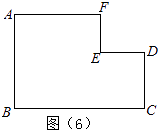
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为4的正方形ABCD内接于点O,点E是 ![]() 上的一动点(不与A、B重合),点F是
上的一动点(不与A、B重合),点F是 ![]() 上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论,其中正确的个数是( ). ①
上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论,其中正确的个数是( ). ① ![]() =
= ![]() ; ②△OGH是等腰三角形; ③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为4+
; ②△OGH是等腰三角形; ③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为4+ ![]() .
.
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com