
【题目】如图,边长为4的正方形ABCD内接于点O,点E是 ![]() 上的一动点(不与A、B重合),点F是
上的一动点(不与A、B重合),点F是 ![]() 上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论,其中正确的个数是( ). ①
上的一点,连接OE、OF,分别与AB、BC交于点G,H,且∠EOF=90°,有以下结论,其中正确的个数是( ). ① ![]() =
= ![]() ; ②△OGH是等腰三角形; ③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为4+
; ②△OGH是等腰三角形; ③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为4+ ![]() .
.
A.1
B.2
C.3
D.4
【答案】B
【解析】解:解:①如图所示,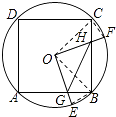
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
在△BOE与△COF中,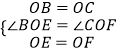
∴△BOE≌△COF,
∴BE=CF,
∴ ![]() =
= ![]() ,①正确;
,①正确;
②∵BE=CF,
∴△BOG≌△COH;
∵∠BOG=∠COH,∠COH+∠OBF=90°,
∴∠GOH=90°,OG=OH,
∴△OGH是等腰直角三角形,②正确.
③如图所示,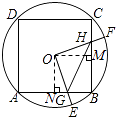
∵△HOM≌△GON,
∴四边形OGBH的面积始终等于正方形ONBM的面积,③错误;
④∵△BOG≌△COH,
∴BG=CH,
∴BG+BH=BC=4,
设BG=x,则BH=4-x,
则GH= ![]() ,
,
∴其最小值为2 ![]() ,D错误.
,D错误.
故选B


科目:初中数学 来源: 题型:
【题目】已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题: 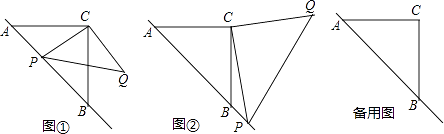
(1)如图①,若点P在线段AB上,且AC=1+ ![]() ,PA=
,PA= ![]() ,则: ①线段PB= , PC=;
,则: ①线段PB= , PC=;
②猜想:PA2 , PB2 , PQ2三者之间的数量关系为;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足 ![]() =
= ![]() ,求
,求 ![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF=∠BAE. 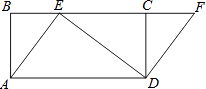
(1)求证:四边形AEFD是平行四边形;
(2)若DF=3,DE=4,AD=5,求CD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O. 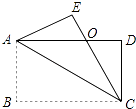
(1)求证:△AOE≌△COD;
(2)若∠OCD=30°,AB= ![]() ,求△AOC的面积.
,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的 ![]() O与边AB相交于点D,DE⊥AC,垂足为点E.
O与边AB相交于点D,DE⊥AC,垂足为点E. 
(1)求证:点D是AB的中点;
(2)判断DE与 ![]() O的位置关系,并证明你的结论;
O的位置关系,并证明你的结论;
(3)若 ![]() O的直径为3,cosB=
O的直径为3,cosB= ![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一渔船自西向东追赶鱼群,在A处测得某无名小岛C在北偏东60°方向上,前进2海里到达B点,此时测得无名小岛C在东北方向上.已知无名小岛周围2.5海里内有暗礁,问渔船继续追赶鱼群有无触礁危险?(参考数据: ![]() =1.414,
=1.414, ![]() =1.732)
=1.732) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
(1)AB的长等于;
(2)在△ABC的内部有一点P,满足S△PAB:S△PBC:S△PCA=1:2:3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明) ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AE⊥CD,垂足为E,AF⊥BC,垂足为F,AD=4,BF=3,∠EAF=60°,设 ![]() =
= ![]() ,如果向量
,如果向量 ![]() =k
=k ![]() (k≠0),那么k的值是 .
(k≠0),那么k的值是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com