
【题目】如图,已知梯形ABCD中,AD∥BC,AB=4,AD=3,AB⊥AC,AC平分∠DCB,过点DE∥AB,分别交AC、BC于F、E,设 ![]() =
= ![]() ,
, ![]() =
= ![]() .求:
.求: 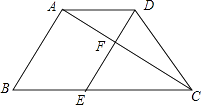
(1)向量 ![]() (用向量
(用向量 ![]() 、
、 ![]() 表示);
表示);
(2)tanB的值.
【答案】
(1)解:∵AD∥BC,
∴∠DAC=∠ACB,
∴AC平分∠DCB,
∴∠DCA=∠ACB,
∴∠DAC=∠DCA,
∴AD=DC,
∵DE∥AB,AB⊥AC,
∴DE⊥AC,
∴AF=CF,
∴BE=CE,
∵AD∥BC,DE∥AB,
∴四边形ABED是平行四边形,
∴DE=AB,
∴ ![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]()
![]() =
= ![]()
![]() ,
,
∴ ![]() =
= ![]() +
+ ![]()
![]() .
.
(2)解:∵∠DCF=∠ACB,∠DFC=∠BAC=90°,
∴△DFC∽△BAC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵CD=AD=3,∴BC=6,
在Rt△BAC中,∠BAC=90°,
∴AC= ![]() =
= ![]() =2
=2 ![]() ,
,
∴tanB= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)首先证明四边形ABED是平行四边形,推出DE=AB,推出 ![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]()
![]() =
= ![]()
![]() ,
, ![]() =
= ![]() +
+ ![]()
![]() .(2)由△DFC∽△BAC,推出
.(2)由△DFC∽△BAC,推出 ![]() =
= ![]() =
= ![]() ,求出BC,在Rt△BAC中,∠BAC=90°,根据AC=
,求出BC,在Rt△BAC中,∠BAC=90°,根据AC= ![]() =
= ![]() =2
=2 ![]() ,由tanB=
,由tanB= ![]() ,即可解决问题.
,即可解决问题.
【考点精析】根据题目的已知条件,利用梯形的定义和解直角三角形的相关知识可以得到问题的答案,需要掌握一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为 ![]() 的线段的概率为( )
的线段的概率为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F在函数y= ![]() (x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是 , △OEF的面积是(用含m的式子表示)
(x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是 , △OEF的面积是(用含m的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AC与BD交于O点,DO:BO=1:2,点E在CB的延长线上,如果S△AOD:S△ABE=1:3,那么BC:BE= . 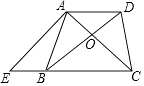
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,AB=AC=5,BC=8,∠PDQ的顶点D在BC边上,DP交AB边于点E,DQ交AB边于点O且交CA的延长线于点F(点F与点A不重合),设∠PDQ=∠B,BD=3.
(1)求证:△BDE∽△CFD;
(2)设BE=x,OA=y,求y关于x的函数关系式,并写出定义域;
(3)当△AOF是等腰三角形时,求BE的长.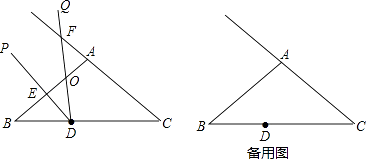
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定: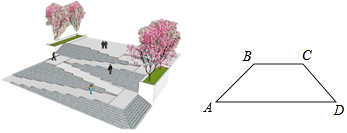
坡度 | 1:20 | 1:16 | 1:12 |
最大高度(米) | 1.50 | 1.00 | 0.75 |
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O. 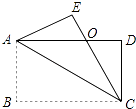
(1)求证:△AOE≌△COD;
(2)若∠OCD=30°,AB= ![]() ,求△AOC的面积.
,求△AOC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com