
【题目】提出问题:
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;
综合运用:
(3)在(2)问条件下,HF∥GE,如图3所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积.
【答案】
(1)
解:∵四边形ABCD是正方形,
∴AB=DA,∠ABE=90°=∠DAH.
∴∠HAO+∠OAD=90°.
∵AE⊥DH,
∴∠ADO+∠OAD=90°.
∴∠HAO=∠ADO.
∴△ABE≌△DAH(ASA),
∴AE=DH
(2)
解:EF=GH.
将FE平移到AM处,则AM∥EF,AM=EF.
将GH平移到DN处,则DN∥GH,DN=GH.

∵EF⊥GH,
∴AM⊥DN,
根据(1)的结论得AM=DN,所以EF=GH
(3)
解:∵四边形ABCD是正方形,
∴AB∥CD
∴∠AHO=∠CGO
∵FH∥EG
∴∠FHO=∠EGO
∴∠AHF=∠CGE
∴△AHF∽△CGE
∴ ![]()
∵EC=2
∴AF=1
过F作FP⊥BC于P,

根据勾股定理得EF= ![]() ,
,
∵FH∥EG,
∴ ![]()
根据(2)知EF=GH,
∴FO=HO.
∴ ![]() ,
,
![]() ,
,
∴阴影部分面积为 ![]() .
.
【解析】(1)由正方形的性质得AB=DA,∠ABE=90°=∠DAH.所以∠HAO+∠OAD=90°,又知∠ADO+∠OAD=90°,所以∠HAO=∠ADO,于是△ABE≌△DAH,可得AE=DH;(2)EF=GH.将FE平移到AM处,则AM∥EF,AM=EF,将GH平移到DN处,则DN∥GH,DN=GH.根据(1)的结论得AM=DN,所以EF=GH;(3)易得△AHF∽△CGE,所以 ![]() ,由EC=2得AF=1,过F作FP⊥BC于P,根据勾股定理得EF=
,由EC=2得AF=1,过F作FP⊥BC于P,根据勾股定理得EF= ![]() ,因为FH∥EG,所以
,因为FH∥EG,所以 ![]() ,根据(2)①知EF=GH,所以FO=HO,再求得三角形FOH与三角形EOG的面积相加即可.
,根据(2)①知EF=GH,所以FO=HO,再求得三角形FOH与三角形EOG的面积相加即可.


科目:初中数学 来源: 题型:
【题目】甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示. 
(1)求甲行走的速度;
(2)在坐标系中,补画s关于t的函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F,已知点A的坐标为(﹣1,0). 
(1)求该抛物线的解析式及顶点M的坐标.
(2)求△EMF与△BNF的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本中有一道作业题: 有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.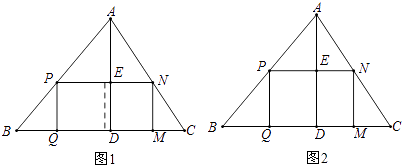
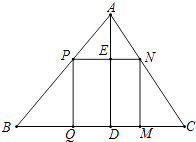
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F在函数y= ![]() (x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是 , △OEF的面积是(用含m的式子表示)
(x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是 , △OEF的面积是(用含m的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路. 
(1)求改直的公路AB的长;
(2)问公路改直后比原来缩短了多少千米?(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AC与BD交于O点,DO:BO=1:2,点E在CB的延长线上,如果S△AOD:S△ABE=1:3,那么BC:BE= . 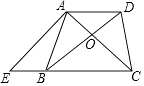
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题: 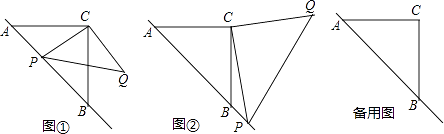
(1)如图①,若点P在线段AB上,且AC=1+ ![]() ,PA=
,PA= ![]() ,则: ①线段PB= , PC=;
,则: ①线段PB= , PC=;
②猜想:PA2 , PB2 , PQ2三者之间的数量关系为;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足 ![]() =
= ![]() ,求
,求 ![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com