
【题目】如图,抛物线y=﹣x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F,已知点A的坐标为(﹣1,0). 
(1)求该抛物线的解析式及顶点M的坐标.
(2)求△EMF与△BNF的面积之比.
【答案】
(1)解:由题意可得:﹣(﹣1)2+2×(﹣1)+c=0,
解得:c=3,
∴y=﹣x2+2x+3,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点M(1,4)
(2)解:∵A(﹣1,0),抛物线的对称轴为直线x=1,
∴点B(3,0),
∴EM=1,BN=2,
∵EM∥BN,
∴△EMF∽△BNF,
∴ ![]() =(
=( ![]() )2=(
)2=( ![]() )2=
)2= ![]() .
.
【解析】(1)直接将(﹣1,0)代入求出即可,再利用配方法求出顶点坐标;(2)利用EM∥BN,则△EMF∽△BNF,进而求出△EMF与△BNE的面积之比.
【考点精析】掌握二次函数的性质和抛物线与坐标轴的交点是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D. 
(1)求证:PO平分∠APC;
(2)连接DB,若∠C=30°,求证:DB∥AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2为同一长方体房间的示意图,图3为该长方体的表面展开图. 
(1)蜘蛛在顶点A′处. ①苍蝇在顶点B处时,试在图1中画出蜘蛛为捉住苍蝇,沿墙面爬行的最近路线.
②苍蝇在顶点C处时,图2中画出了蜘蛛捉住苍蝇的两条路线,往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC,试通过计算判断哪条路线更近.
(2)在图3中,半径为10dm的⊙M与D′C′相切,圆心M到边CC′的距离为15dm,蜘蛛P在线段AB上,苍蝇Q在⊙M的圆周上,线段PQ为蜘蛛爬行路线,若PQ与⊙M相切,试求PQ长度的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设函数y=(x﹣1)[(k﹣1)x+(k﹣3)](k是常数). 
(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时的函数的图象;
(2)根据图象,写出你发现的一条结论;
(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到的函数y3的图象,求函数y3的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班五位同学参加学校举办的数学素养竞赛.试卷中共有20道题,规定每题答对得5分,答错扣2分,未答得0分.赛后A,B,C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表
参赛同学 | 答对题数 | 答错题数 | 未答题数 |
A | 19 | 0 | 1 |
B | 17 | 2 | 1 |
C | 15 | 2 | 3 |
D | 17 | 1 | 2 |
E | / | / | 7 |
(1)根据以上信息,求A,B,C,D四位同学成绩的平均分;
(2)最后获知A,B,C,D,E五位同学成绩分别是95分,81分,64分,83分,58分. ①求E同学的答对题数和答错题数;
②经计算,A,B,C,D四位同学实际成绩的平均分是80.75分,与(1)中算得的平均分不相符,发现是其中一位同学记错了自己的答题情况,请指出哪位同学记错了,并写出他的实际答题情况(直接写出答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某翼装飞行员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC(结果精确到1m).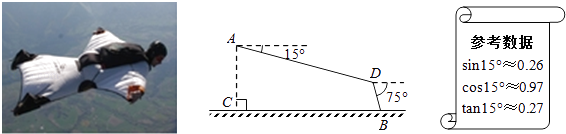
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为n的正方形OABC的边OA,OC在坐标轴上,点A1 , A2 , …,An﹣1为OA的n等分点,点B1 , B2 , …,Bn﹣1为CB的n等分点,连结A1B1 , A2B2 , …,An﹣1Bn﹣1 , 分别交曲线y= ![]() (x>0)于点C1 , C2 , …,Cn﹣1 . 若C15B15=16C15A15 , 则n的值为 . (n为正整数)
(x>0)于点C1 , C2 , …,Cn﹣1 . 若C15B15=16C15A15 , 则n的值为 . (n为正整数) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;
综合运用:
(3)在(2)问条件下,HF∥GE,如图3所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Word文本中的图形,在图形格式中大小菜单下显示有图形的绝对高度和绝对宽度,同一个图形随其放置方向的变化,所显示的绝对高度和绝对宽度也随之变化.如图①、②、③是同一个三角形以三条不同的边水平放置时,它们所显示的绝对高度和绝对宽度如下表,现有△ABC,已知AB=AC,当它以底边BC水平放置时(如图④),它所显示的绝对高度和绝对宽度如下表,那么当△ABC以腰AB水平放置时(如图⑤),它所显示的绝对高度和绝对宽度分别是( ) 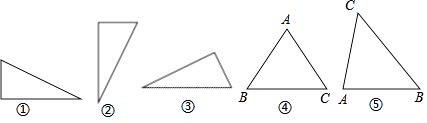
图形 | 图① | 图② | 图③ | 图④ | 图⑤ |
绝对高度 | 1.50 | 2.00 | 1.20 | 2.40 | ? |
绝对宽度 | 2.00 | 1.50 | 2.50 | 3.60 | ? |
A.3.60和2.40
B.2.56和3.00
C.2.56和2.88
D.2.88和3.00
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com