
【题目】图1、图2为同一长方体房间的示意图,图3为该长方体的表面展开图. 
(1)蜘蛛在顶点A′处. ①苍蝇在顶点B处时,试在图1中画出蜘蛛为捉住苍蝇,沿墙面爬行的最近路线.
②苍蝇在顶点C处时,图2中画出了蜘蛛捉住苍蝇的两条路线,往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC,试通过计算判断哪条路线更近.
(2)在图3中,半径为10dm的⊙M与D′C′相切,圆心M到边CC′的距离为15dm,蜘蛛P在线段AB上,苍蝇Q在⊙M的圆周上,线段PQ为蜘蛛爬行路线,若PQ与⊙M相切,试求PQ长度的范围.
【答案】
(1)解:①根据“两点之间,线段最短”可知:
线段A′B为最近路线,如图1所示.

②(i).将长方体展开,使得长方形ABB′A′和长方形ABCD在同一平面内,如图2①.
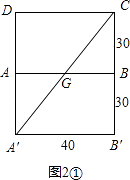
在Rt△A′B′C中,
∠B′=90°,A′B′=40,B′C=60,
∴AC= ![]() =
= ![]() =20
=20 ![]() .
.
(ii).将长方体展开,使得长方形ABB′A′和长方形BCC′B′在同一平面内,如图2②.
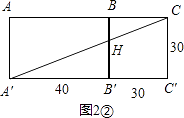
在Rt△A′C′C中,
∠C′=90°,A′C′=70,C′C=30,
∴A′C= ![]() =
= ![]() =10
=10 ![]() .
.
∵ ![]() <
< ![]() ,
,
∴往天花板ABCD爬行的最近路线A′GC更近
(2)解:过点M作MH⊥AB于H,连接MQ、MP、MA、MB,如图3.
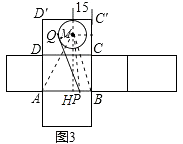
∵半径为10dm的⊙M与D′C′相切,圆心M到边CC′的距离为15dm,BC′=60dm,
∴MH=60﹣10=50,HB=15,AH=40﹣15=25,
根据勾股定理可得AM= ![]() =
= ![]() =
= ![]() ,
,
MB= ![]() =
= ![]() =
= ![]() ,
,
∴50≤MP≤ ![]() .
.
∵⊙M与PQ相切于点Q,
∴MQ⊥PQ,∠MQP=90°,
∴PQ= ![]() =
= ![]() .
.
当MP=50时,PQ= ![]() =20
=20 ![]() ;
;
当MP= ![]() 时,PQ=
时,PQ= ![]() =55.
=55.
∴PQ长度的范围是20 ![]() dm≤PQ≤55dm
dm≤PQ≤55dm
【解析】(1)①根据“两点之间,线段最短”可知:线段A′B为最近路线; ②(i).将长方体展开,使得长方形ABB′A′和长方形ABCD在同一平面内,如图2①,运用勾股定理求出AC长;(ii).将长方体展开,使得长方形ABB′A′和长方形BCC′B′在同一平面内,如图2②,运用勾股定理求出A′C长,然后将两个长度进行比较,就可解决问题;(2)过点M作MH⊥AB于H,连接MQ、MP、MA、MB,如图3.由⊙M与PQ相切于点Q可得MQ⊥PQ,即∠MQP=90°,根据勾股定理可得PQ= ![]() =
= ![]() .要求PQ的取值范围,只需先求出MP的取值范围,就可解决问题.
.要求PQ的取值范围,只需先求出MP的取值范围,就可解决问题.
【考点精析】关于本题考查的几何体的展开图和线段的基本性质,需要了解沿多面体的棱将多面体剪开成平面图形,若干个平面图形也可以围成一个多面体;同一个多面体沿不同的棱剪开,得到的平面展开图是不一样的,就是说:同一个立体图形可以有多种不同的展开图;线段公理:所有连接两点的线中,线段最短.也可简单说成:两点之间线段最短;连接两点的线段的长度,叫做这两点的距离;线段的大小关系和它们的长度的大小关系是一致的才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系. 
(1)活动中心与小宇家相距千米,小宇在活动中心活动时间为小时,他从活动中心返家时,步行用了小时;
(2)求线段BC所表示的y(千米)与x(小时)之间的函数关系式(不必写出x所表示的范围);
(3)根据上述情况(不考虑其他因素),请判断小宇是否能在12:00前回到家,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.
(1)求抛物线的函数表达式;
(2)若点D是y轴上的一点,且以B,C,D为顶点的三角形与△ABC相似,求点D的坐标;
(3)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标及最大面积;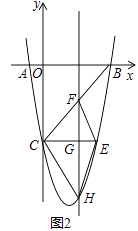
(4)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示. 
(1)求甲行走的速度;
(2)在坐标系中,补画s关于t的函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABC1D1的边长为1,延长C1D1到A1 , 以A1C1为边向右作正方形A1C1C2D2 , 延长C2D2到A2 , 以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推….若A1C1=2,且点A,D2 , D3 , …,D10都在同一直线上,则正方形A9C9C10D10的边长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为 ![]() 的线段的概率为( )
的线段的概率为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F,已知点A的坐标为(﹣1,0). 
(1)求该抛物线的解析式及顶点M的坐标.
(2)求△EMF与△BNF的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AC与BD交于O点,DO:BO=1:2,点E在CB的延长线上,如果S△AOD:S△ABE=1:3,那么BC:BE= . 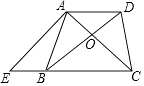
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com