
����Ŀ��ij��������8��00С��Ӽҳ������˳�1Сʱ����ij����IJμ�ʵ�����11��00ʱ���ڻ���Ľӵ��ְֵĵ绰������Ҫ������12��00ǰ�ص��ң������̰����������ʱ��·�ߣ���5ǧ��/Сʱ��ƽ���ٶȿ첽���أ�ͬʱ���ְִӼ���ͬһ·�߿����������ھ��20ǧ�״�������С���������ԭ���ij���ԭ·���أ���С�����x��Сʱ���������y��ǧ�ף��ĵط���ͼ������OABCD��ʾy��x֮��ĺ�����ϵ�� 
��1���������С������ǧ�ף�С���ڻ���Ļʱ��ΪСʱ�����ӻ���ķ���ʱ����������Сʱ��
��2�����߶�BC����ʾ��y��ǧ�ף���x��Сʱ��֮��ĺ�����ϵʽ������д��x����ʾ�ķ�Χ����
��3����������������������������أ������ж�С���Ƿ�����12��00ǰ�ص��ң���˵�����ɣ�
���𰸡�
��1��22��2��0.4
��2���⣺��������ã�y=22��5��x��3��=��5x+37
��3���⣺С��ӻ���ķ�������ʱ��Ϊ��0.4+0.4=0.8��Сʱ����
��0.8��1��
������С��12��00ǰ�ܵ���
���������⣺��1���ߵ�A������Ϊ��1��22������B������Ϊ��3��22���� ��������С������22ǧ�ף�С���ڻ���Ļʱ��Ϊ3��1=2Сʱ��
��22��20����5=0.4��Сʱ����
���Դ��ǣ�22��2��0.4��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���DAC=��ACB��Ҫʹ�ı���ABCD��Ϊƽ���ı��Σ���Ӧ���ӵ����������ǣ� �� 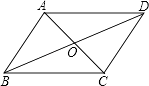
A.AD=BC
B.OA=OC
C.AB=CD
D.��ABC+��BCD=180��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��һ�ž���ֽƬABCD������AD=8cm��AB=6cm�����ضԽ���BD���ۣ���C���ڵ�C���λ�ã�BC�佻AD�ڵ�G�� 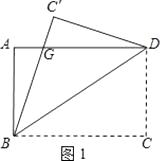
��1����֤��AG=C��G��
��2����ͼ2�����۵�һ�Σ�ʹ��D���A�غϣ����ۺ�EN��EN��AD�ڵ�M����EM�ij��� 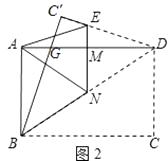
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ6cm��������ABCD�У���E��F��G��H�ֱ�ӵ�A��B��C��Dͬʱ����������1cm/s���ٶ����B��C��D��A�����˶�������E�����Bʱ���ĸ���ͬʱֹͣ�˶������˶������У����˶�ʱ��Ϊsʱ���ı���EFGH�������С������Сֵ��cm2 �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx��2��x�ύ��A��B���㣬��y�ύ��C�㣬��֪A��3��0������M��1���� ![]() ��������������һ�㣮
��������������һ�㣮
��1����a��b��ֵ��
��2������AC�����P��y������һ�㣬����P��A��C����Ϊ������������ǵ��������Σ���P������ꣻ
��3������N��x���������������������ڵ�һ���㣨����O��A�غϣ�������N��NH��AC�������ߵĶԳ�����H�㣮��ON=t����ONH�����ΪS����S��t֮��ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ3����E�ڱ�AB�ϣ���BE=1������P�ڶԽ���BD���ƶ�����PA+PE����Сֵ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PA��PB�ǡ�O�����ߣ�A��BΪ�е㣬����AO���ӳ�����PB���ӳ����ڵ�C������PO������O�ڵ�D�� 
��1����֤��POƽ�֡�APC��
��2������DB������C=30�㣬��֤��DB��AC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��ͼ2Ϊͬһ�����巿���ʾ��ͼ��ͼ3Ϊ�ó�����ı���չ��ͼ�� 
��1��֩���ڶ���A�䴦�� �ٲ�Ӭ�ڶ���B��ʱ������ͼ1�л���֩��Ϊס��Ӭ����ǽ�����е����·�ߣ�
�ڲ�Ӭ�ڶ���C��ʱ��ͼ2�л�����֩��ס��Ӭ������·�ߣ����컨��ABCD���е����·��A��GC����ǽ��BB��C��C���е����·��A��HC����ͨ�������ж�����·�߸�����
��2����ͼ3�У��뾶Ϊ10dm�ġ�M��D��C�����У�Բ��M����CC��ľ���Ϊ15dm��֩��P���߶�AB�ϣ���ӬQ�ڡ�M��Բ���ϣ��߶�PQΪ֩������·�ߣ���PQ���M���У�����PQ���ȵķ�Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com