
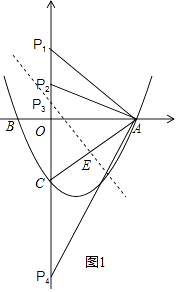
����Ŀ����ͼ��������y=ax2+bx��2��x�ύ��A��B���㣬��y�ύ��C�㣬��֪A��3��0������M��1���� ![]() ��������������һ�㣮
��������������һ�㣮
��1����a��b��ֵ��
��2������AC�����P��y������һ�㣬����P��A��C����Ϊ������������ǵ��������Σ���P������ꣻ
��3������N��x���������������������ڵ�һ���㣨����O��A�غϣ�������N��NH��AC�������ߵĶԳ�����H�㣮��ON=t����ONH�����ΪS����S��t֮��ĺ�����ϵʽ��
���𰸡�
��1��
�⣺��A��3��0������M��1���� ![]() ������y=ax2+bx��2��
������y=ax2+bx��2�� 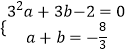 ��
��
��ã� 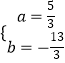
��2��
�⣺��y=ax2+bx��2�У���x=0ʱ��y=��2��
��C��0����2����
��OC=2��
��ͼ����P��0��m������PC=m+2��OA=3��AC= ![]() =
= ![]() ��
��
�ٵ�PA=CAʱ����OP1=OC=2��
��P1��0��2����
�ڵ�PC=CA= ![]() ʱ����m+2=
ʱ����m+2= ![]() ����m=
����m= ![]() ��2��
��2��
��P2��0�� ![]() ��2����
��2����
�۵�PC=PAʱ����P��AC�Ĵ�ֱƽ�����ϣ�
���AOC�ס�P3EC��
�� ![]() =
= ![]() ��
��
��P3C= ![]() ��
��
��m= ![]() ��
��
��P3��0�� ![]() ����
����
�ܵ�PC=CA= ![]() ʱ��m=��2��
ʱ��m=��2�� ![]() ��
��
��P4��0����2�� ![]() ����
����
����������P�������1��0��2����0�� ![]() ��2����0��
��2����0�� ![]() ����0����2��
����0����2�� ![]() ��
��
��3��
�⣺��H��HG��OA��G����HN��Y����M��
��NH��AC��
�� ![]() ��
��
�� ![]() ��
��
��OM= ![]() ��
��
�������ߵĶԳ���Ϊֱ��x= ![]() =
= ![]() ��
��
��OG= ![]() ��
��
��GN=t�� ![]() ��
��
��GH��OC��
���NGH�ס�NOM��
�� ![]() ��
��
�� ![]() =
= ![]() ��
��
��HG= ![]() t��
t�� ![]() ��
��
��S= ![]() ONGH=
ONGH= ![]() t��
t�� ![]() t��
t�� ![]() ��=
��= ![]() t2��
t2�� ![]() t��0��t��3����
t��0��t��3����
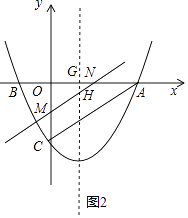
����������1�����������з����鼴�ɵõ����ۣ���2����y=ax2+bx��2�У���x=0ʱ��y=��2���õ�OC=2����ͼ����P��0��m������PC=m+2��OA=3�����ݹ��ɶ����õ�AC= ![]() =
= ![]() ���ٵ�PA=CAʱ����OP1=OC=2���ڵ�PC=CA=
���ٵ�PA=CAʱ����OP1=OC=2���ڵ�PC=CA= ![]() ʱ���۵�PC=PAʱ����P��AC�Ĵ�ֱƽ�����ϣ��������������ε����ʵõ�P3��0��
ʱ���۵�PC=PAʱ����P��AC�Ĵ�ֱƽ�����ϣ��������������ε����ʵõ�P3��0�� ![]() �����ܵ�PC=CA=
�����ܵ�PC=CA= ![]() ʱ�����ǵõ����ۣ���3����H��HG��OA��G����HN��Y����M������ƽ���߷��߶γɱ��������õ�OM=
ʱ�����ǵõ����ۣ���3����H��HG��OA��G����HN��Y����M������ƽ���߷��߶γɱ��������õ�OM= ![]() ����������ߵĶԳ���Ϊֱ��x=
����������ߵĶԳ���Ϊֱ��x= ![]() =
= ![]() ���õ�OG=
���õ�OG= ![]() �����GN=t��
�����GN=t�� ![]() ���������������ε����ʵõ�HG=
���������������ε����ʵõ�HG= ![]() t��
t�� ![]() �����ǵõ����ۣ�
�����ǵõ����ۣ�
�����㾫����������Ŀ����֪���������ù��ɶ����ĸ����ƽ���߷��߶γɱ��������֪ʶ���Եõ�����Ĵ𰸣���Ҫ����ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2������ƽ���߽�����ֱ�ߣ����õĶ�Ӧ�߶γɱ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��45�㣼��A��90�㣬�����и�ʽ�������ǣ� �� 
A.sinA=cosA
B.sinA��cosA
C.sinA��tanA
D.sinA��cosA
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У����κ���y=�� ![]() +bx+c��ͼ����A��1��0�����ҵ�x=0��x=5ʱ����Ӧ�ĺ���ֵ��ȣ�һ�κ���y=��x+3����κ���y=��
+bx+c��ͼ����A��1��0�����ҵ�x=0��x=5ʱ����Ӧ�ĺ���ֵ��ȣ�һ�κ���y=��x+3����κ���y=�� ![]() +bx+c��ͼ��ֱ���B��C���㣬��B�ڵ�һ���ޣ�
+bx+c��ͼ��ֱ���B��C���㣬��B�ڵ�һ���ޣ�
��1������κ���y=�� ![]() +bx+c�ı���ʽ��
+bx+c�ı���ʽ��
��2������AB����AB�ij���
��3������AC��M���߶�AC���е㣬����B�Ƶ�M��ת180��õ���N������AN��CN���ж��ı���ABCN����״����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������8��00С��Ӽҳ������˳�1Сʱ����ij����IJμ�ʵ�����11��00ʱ���ڻ���Ľӵ��ְֵĵ绰������Ҫ������12��00ǰ�ص��ң������̰����������ʱ��·�ߣ���5ǧ��/Сʱ��ƽ���ٶȿ첽���أ�ͬʱ���ְִӼ���ͬһ·�߿����������ھ��20ǧ�״�������С���������ԭ���ij���ԭ·���أ���С�����x��Сʱ���������y��ǧ�ף��ĵط���ͼ������OABCD��ʾy��x֮��ĺ�����ϵ�� 
��1���������С������ǧ�ף�С���ڻ���Ļʱ��ΪСʱ�����ӻ���ķ���ʱ����������Сʱ��
��2�����߶�BC����ʾ��y��ǧ�ף���x��Сʱ��֮��ĺ�����ϵʽ������д��x����ʾ�ķ�Χ����
��3����������������������������أ������ж�С���Ƿ�����12��00ǰ�ص��ң���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=6cm��BC=2cm����P�ڱ�AC�ϣ��ӵ�A���C�ƶ�����Q�ڱ�CB�ϣ��ӵ�C���B�ƶ�������P��Q����1cm/s���ٶ�ͬʱ�������ҵ�һ���ƶ����յ�ʱ����һ��Ҳ��ֹ֮ͣ������PQ�����߶�PQ����Сֵ�ǣ� �� 
A.20cm
B.18cm
C.2 ![]() cm
cm
D.3 ![]() cm
cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB���O�����ڵ�B��BCΪ��O���ң�OC��OA��OA��BC�ཻ�ڵ�P�� 
��1����֤��AP=AB��
��2����OB=4��AB=3�����߶�BP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B�����ڷ���������y= ![]() ��ͼ���ϣ�C��D�����ڷ���������y=
��ͼ���ϣ�C��D�����ڷ���������y= ![]() ��ͼ���ϣ�AC��y���ڵ�E��BD��y���ڵ�F��AC=2��BD=1��EF=3����k1��k2��ֵ�ǣ� ��
��ͼ���ϣ�AC��y���ڵ�E��BD��y���ڵ�F��AC=2��BD=1��EF=3����k1��k2��ֵ�ǣ� �� 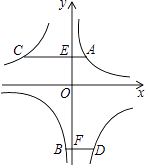
A.6
B.4
C.3
D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABC1D1�ı߳�Ϊ1���ӳ�C1D1��A1 �� ��A1C1Ϊ��������������A1C1C2D2 �� �ӳ�C2D2��A2 �� ��A2C2Ϊ��������������A2C2C3D3����ͼ��ʾ�����Դ����ơ�����A1C1=2���ҵ�A��D2 �� D3 �� ����D10����ͬһֱ���ϣ���������A9C9C10D10�ı߳��� �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com