
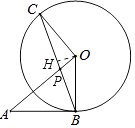
【题目】如图,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P. 
(1)求证:AP=AB;
(2)若OB=4,AB=3,求线段BP的长.
【答案】
(1)证明:∵OC=OB,
∴∠OCB=∠OBC,
∴AB是⊙O的切线,
∴OB⊥AB,
∴∠OBA=90°,
∴∠ABP+∠OBC=90°,
∵OC⊥AO,
∴∠AOC=90°,
∴∠OCB+∠CPO=90°,
∵∠APB=∠CPO,
∴∠APB=∠ABP,
∴AP=AB
(2)解:作OH⊥BC于H.
在Rt△OAB中,∵OB=4,AB=3,
∴OA= ![]() =5,
=5,
∵AP=AB=3,
∴PO=2.
在Rt△POC中,PC= ![]() =2
=2 ![]() ,
,
∵ ![]() PCOH=
PCOH= ![]() OCOP,
OCOP,
∴OH= ![]() =
= ![]() ,
,
∴CH= ![]() =
= ![]() ,
,
∵OH⊥BC,
∴CH=BH,
∴BC=2CH= ![]() ,
,
∴PB=BC﹣PC= ![]() ﹣2
﹣2 ![]() =
= ![]() .
.
【解析】(1)欲证明AP=AB,只要证明∠APB=∠ABP即可;(2)作OH⊥BC于H.在Rt△POC中,求出OP、PC、OH、CH即可解决问题.
【考点精析】利用切线的性质定理对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】对于坐标平面内的点,现将该点向右平移1个单位,再向上平移2的单位,这种点的运动称为点A的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5),已知点A的坐标为(1,0).
(1)分别写出点A经1次,2次斜平移后得到的点的坐标.
(2)如图,点M是直线l上的一点,点A关于点M的对称点的点B,点B关于直线l的对称轴为点C.
①若A、B、C三点不在同一条直线上,判断△ABC是否是直角三角形?请说明理由.
②若点B由点A经n次斜平移后得到,且点C的坐标为(7,6),求出点B的坐标及n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣2与x轴交于A、B两点,与y轴交于C点,已知A(3,0),且M(1,﹣ ![]() )是抛物线上另一点.
)是抛物线上另一点.
(1)求a、b的值;
(2)连结AC,设点P是y轴上任一点,若以P、A、C三点为顶点的三角形是等腰三角形,求P点的坐标;
(3)若点N是x轴正半轴上且在抛物线内的一动点(不与O、A重合),过点N作NH∥AC交抛物线的对称轴于H点.设ON=t,△ONH的面积为S,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D. 
(1)求证:PO平分∠APC;
(2)连接DB,若∠C=30°,求证:DB∥AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育”活动,共开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出). 
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设函数y=(x﹣1)[(k﹣1)x+(k﹣3)](k是常数). 
(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时的函数的图象;
(2)根据图象,写出你发现的一条结论;
(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到的函数y3的图象,求函数y3的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com