
【题目】如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D. 
(1)求证:PO平分∠APC;
(2)连接DB,若∠C=30°,求证:DB∥AC.
【答案】
(1)证明:如图,连接OB,
∵PA,PB是⊙O的切线,
∴OA⊥AP,OB⊥BP,
又OA=OB,
∴PO平分∠APC
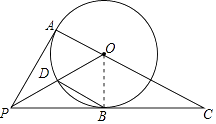
(2)证明:∵OA⊥AP,OB⊥BP,
∴∠CAP=∠OBP=90°,
∵∠C=30°,
∴∠APC=90°﹣∠C=90°﹣30°=60°,
∵PO平分∠APC,
∴∠OPC= ![]() ∠APC=
∠APC= ![]() =30°,
=30°,
∴∠POB=90°﹣∠OPC=90°﹣30°=60°,
又OD=OB,
∴△ODB是等边三角形,
∴∠OBD=60°,
∴∠DBP=∠OBP﹣∠OBD=90°﹣60°=30°,
∴∠DBP=∠C,
∴DB∥AC
【解析】(1)连接OB,根据角平分线性质定理的逆定理,即可解答;(2)先证明△ODB是等边三角形,得到∠OBD=60°,再由∠DBP=∠C,即可得到DB∥AC.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】某中学为了了解学生的体育锻炼情况,随机抽查了部分学生一周参加体育锻炼的时间,得到如图的条形统计图,根据图形解答下列问题: 
(1)这次抽查了名学生;
(2)所抽查的学生一周平均参加体育锻炼多少小时?
(3)已知该校有1200名学生,估计该校有多少名学生一周参加体育锻炼的时间超过6小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系. 
(1)活动中心与小宇家相距千米,小宇在活动中心活动时间为小时,他从活动中心返家时,步行用了小时;
(2)求线段BC所表示的y(千米)与x(小时)之间的函数关系式(不必写出x所表示的范围);
(3)根据上述情况(不考虑其他因素),请判断小宇是否能在12:00前回到家,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P. 
(1)求证:AP=AB;
(2)若OB=4,AB=3,求线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y1=x与y2= ![]() 的图象如图所示,下列关于函数y=y1+y2的结论:①函数的图象关于原点中心对称;②当x<2时,y随x的增大而减小;③当x>0时,函数的图象最低点的坐标是(2,4),其中所有正确结论的序号是 .
的图象如图所示,下列关于函数y=y1+y2的结论:①函数的图象关于原点中心对称;②当x<2时,y随x的增大而减小;③当x>0时,函数的图象最低点的坐标是(2,4),其中所有正确结论的序号是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两点在反比例函数y= ![]() 的图象上,C,D两点在反比例函数y=
的图象上,C,D两点在反比例函数y= ![]() 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1﹣k2的值是( )
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1﹣k2的值是( ) 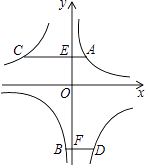
A.6
B.4
C.3
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.
(1)求抛物线的函数表达式;
(2)若点D是y轴上的一点,且以B,C,D为顶点的三角形与△ABC相似,求点D的坐标;
(3)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标及最大面积;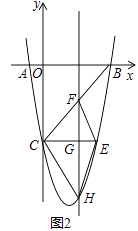
(4)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示. 
(1)求甲行走的速度;
(2)在坐标系中,补画s关于t的函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F,已知点A的坐标为(﹣1,0). 
(1)求该抛物线的解析式及顶点M的坐标.
(2)求△EMF与△BNF的面积之比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com