
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���֪������y=ax2+bx��5��x�ύ��A����1��0����B��5��0�����㣬��y�ύ�ڵ�C��
��1���������ߵĺ�������ʽ��
��2������D��y���ϵ�һ�㣬����B��C��DΪ��������������ABC���ƣ����D�����ꣻ
��3����ͼ2��CE��x�����������ཻ�ڵ�E����H��ֱ��CE�·��������ϵĶ��㣬����H����y��ƽ�е�ֱ����BC��CE�ֱ��ڵ�F��G����̽������H�˶����δ�ʱ���ı���CHEF�����������H�����꼰��������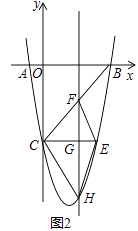
��4������KΪ�����ߵĶ��㣬��M��4��m���Ǹ��������ϵ�һ�㣬��x�ᣬy���Ϸֱ��ҵ�P��Q��ʹ�ı���PQKM���ܳ���С�������P��Q�����꣮
���𰸡�
��1��
�⣺�ߵ�A����1��0����B��5��0����������y=ax2+bx��5�ϣ�
�� ![]() ��
��
�� ![]() ��
��
�������ߵı���ʽΪy=x2��4x��5
��2��
�⣺��ͼ1����x=0����y=��5��
��C��0����5����
��OC=OB��
���OBC=��OCB=45�㣬
��AB=6��BC=5 ![]() ��
��
Ҫʹ��B��C��DΪ��������������ABC���ƣ����� ![]() ��
�� ![]() ��
��
�ٵ� ![]() ʱ��
ʱ��
CD=AB=6��
��D��0��1����
�ڵ� ![]() ʱ��
ʱ��
�� ![]() ��
��
��CD= ![]() ��
��
��D��0�� ![]() ����
����
����D��������0��1����0�� ![]() ��
��

��3��
�⣺��H��t��t2��4t��5����
��CE��x�ᣬ
���E����������5��
��E���������ϣ�
��x2��4x��5=��5����x=0���ᣩ��x=4��
��E��4����5����
��CE=4��
��B��5��0����C��0����5����
��ֱ��BC�Ľ���ʽΪy=x��5��
��F��t��t��5����
��HF=t��5����t2��4t��5��=����t�� ![]() ��2+
��2+ ![]() ��
��
��CE��x�ᣬHF��y�ᣬ
��CE��HF��
��S�ı���CHEF= ![]() CEHF=��2��t��
CEHF=��2��t�� ![]() ��2+
��2+ ![]() ��
��
��t= ![]() ʱ���ı���CHEF��������Ϊ
ʱ���ı���CHEF��������Ϊ ![]()
��4��
�⣺��ͼ2����KΪ�����ߵĶ��㣬
��K��2����9����
��K����y��ĶԳƵ�K'����2����9����
��M��4��m�����������ϣ�
��M��4����5����
���M����x��ĶԳƵ�M'��4��5����
��ֱ��K'M'�Ľ���ʽΪy= ![]() x��
x�� ![]() ��
��
��P�� ![]() ��0����Q��0����
��0����Q��0���� ![]() ����
����

����������1�����ݴ���ϵ����ֱ�������߽���ʽ����2��������������������������εı���ʽ���������D�����ꣻ��3�������ֱ��BC�Ľ���ʽ����������ı���CHEF������ĺ�����ϵʽ������������ֵ����4�����öԳ����ҳ���P��Q��λ�ã��������P��Q�����꣮
�����㾫����������Ҫ�����˶��κ��������ʺ����������ε����ʵ����֪ʶ�㣬��Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С����Ӧ����ȣ���Ӧ�߳ɱ��������������ν������������β�����ȷ�����⣮


 С��ſ�ʱ��ҵϵ�д�
С��ſ�ʱ��ҵϵ�д� һ������ϵ�д�
һ������ϵ�д� �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��һ�ž���ֽƬABCD������AD=8cm��AB=6cm�����ضԽ���BD���ۣ���C���ڵ�C���λ�ã�BC�佻AD�ڵ�G�� 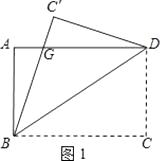
��1����֤��AG=C��G��
��2����ͼ2�����۵�һ�Σ�ʹ��D���A�غϣ����ۺ�EN��EN��AD�ڵ�M����EM�ij��� 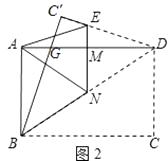
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ3����E�ڱ�AB�ϣ���BE=1������P�ڶԽ���BD���ƶ�����PA+PE����Сֵ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PA��PB�ǡ�O�����ߣ�A��BΪ�е㣬����AO���ӳ�����PB���ӳ����ڵ�C������PO������O�ڵ�D�� 
��1����֤��POƽ�֡�APC��
��2������DB������C=30�㣬��֤��DB��AC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������չ��������������������������������������ܲ������˶���Ŀ��Ϊ�˽�ѧ����ϲ����һ����Ŀ�������ȡ�˲���ѧ�����е��飬�����������µ�����ͳ��ͼ������ͳ��ͼ��������Ϣδ�������� 
��1���α������ѧ��������
��2����ȫ����ͳ��ͼ��
��3����У����1200��ѧ���������ȫУ��ϲ���������������ϲ���������������٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڷ���ֽ�У��߶�a��b��c��d�Ķ˵��ڸ���ϣ�ͨ��ƽ�����������߶Σ�ʹ�ú͵������߶���β�����������Σ�������������εIJ�ͬƽ�Ʒ����У� �� 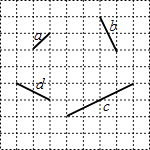
A.3��
B.6��
C.8��
D.12��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��ͼ2Ϊͬһ�����巿���ʾ��ͼ��ͼ3Ϊ�ó�����ı���չ��ͼ�� 
��1��֩���ڶ���A�䴦�� �ٲ�Ӭ�ڶ���B��ʱ������ͼ1�л���֩��Ϊס��Ӭ����ǽ�����е����·�ߣ�
�ڲ�Ӭ�ڶ���C��ʱ��ͼ2�л�����֩��ס��Ӭ������·�ߣ����컨��ABCD���е����·��A��GC����ǽ��BB��C��C���е����·��A��HC����ͨ�������ж�����·�߸�����
��2����ͼ3�У��뾶Ϊ10dm�ġ�M��D��C�����У�Բ��M����CC��ľ���Ϊ15dm��֩��P���߶�AB�ϣ���ӬQ�ڡ�M��Բ���ϣ��߶�PQΪ֩������·�ߣ���PQ���M���У�����PQ���ȵķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊn��������OABC�ı�OA��OC���������ϣ���A1 �� A2 �� ����An��1ΪOA��n�ȷֵ㣬��B1 �� B2 �� ����Bn��1ΪCB��n�ȷֵ㣬����A1B1 �� A2B2 �� ����An��1Bn��1 �� �ֱ�����y= ![]() ��x��0���ڵ�C1 �� C2 �� ����Cn��1 �� ��C15B15=16C15A15 �� ��n��ֵΪ �� ��nΪ��������
��x��0���ڵ�C1 �� C2 �� ����Cn��1 �� ��C15B15=16C15A15 �� ��n��ֵΪ �� ��nΪ�������� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com