
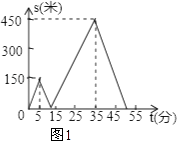
【题目】甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示. 
(1)求甲行走的速度;
(2)在坐标系中,补画s关于t的函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
【答案】
(1)解:甲行走的速度:150÷5=30(米/分)
(2)解:当t=35时,甲行走的路程为:30×35=1050(米),乙行走的路程为:(35﹣5)×50=1500(米),
∴当t=35时,乙已经到达图书馆,甲距图书馆的路程还有(1500﹣1050)=450米,
∴甲到达图书馆还需时间;450÷30=15(分),
∴35+15=50(分),
∴当s=0时,横轴上对应的时间为50.
补画的图象如图所示(横轴上对应的时间为50),
(3)解:如图2,
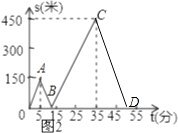
设乙出发经过x分和甲第一次相遇,根据题意得:150+30x=50x,
解得:x=7.5,
7.5+5=12.5(分),
由函数图象可知,当t=12.5时,s=0,
∴点B的坐标为(12.5,0),
当12.5≤t≤35时,设BC的解析式为:s=kt+b,(k≠0),
把C(35,450),B(12.5,0)代入可得: ![]()
解得: ![]() ,
,
∴s=20t﹣250,
当35<t≤50时,设CD的解析式为s=k1x+b1,(k1≠0),
把D(50,0),C(35,450)代入得: ![]()
解得: ![]()
∴s=﹣30t+1500,
∵甲、乙两人相距360米,即s=360,
解得:t1=30.5,t2=38,
∴当甲行走30.5分钟或38分钟时,甲、乙两人相距360米
【解析】(1)由图象可知t=5时,s=150米,根据速度=路程÷时间,即可解答;(2)根据图象提供的信息,可知当t=35时,乙已经到达图书馆,甲距图书馆的路程还有(1500﹣1050)=450米,甲到达图书馆还需时间;450÷30=15(分),所以35+15=50(分),所以当s=0时,横轴上对应的时间为50.(3)分别求出当12.5≤t≤35时和当35<t≤50时的函数解析式,根据甲、乙两人相距360米,即s=360,分别求出t的值即可.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D. 
(1)求证:PO平分∠APC;
(2)连接DB,若∠C=30°,求证:DB∥AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育”活动,共开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出). 
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有( ) 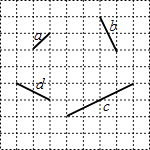
A.3种
B.6种
C.8种
D.12种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y= ![]() (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .
(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2为同一长方体房间的示意图,图3为该长方体的表面展开图. 
(1)蜘蛛在顶点A′处. ①苍蝇在顶点B处时,试在图1中画出蜘蛛为捉住苍蝇,沿墙面爬行的最近路线.
②苍蝇在顶点C处时,图2中画出了蜘蛛捉住苍蝇的两条路线,往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC,试通过计算判断哪条路线更近.
(2)在图3中,半径为10dm的⊙M与D′C′相切,圆心M到边CC′的距离为15dm,蜘蛛P在线段AB上,苍蝇Q在⊙M的圆周上,线段PQ为蜘蛛爬行路线,若PQ与⊙M相切,试求PQ长度的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设函数y=(x﹣1)[(k﹣1)x+(k﹣3)](k是常数). 
(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时的函数的图象;
(2)根据图象,写出你发现的一条结论;
(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到的函数y3的图象,求函数y3的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;
综合运用:
(3)在(2)问条件下,HF∥GE,如图3所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com