
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y= ![]() (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .
(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 . 
【答案】(12, ![]() )
)
【解析】解:过点D作DM⊥x轴于点M,过点F作FE⊥x于点E, 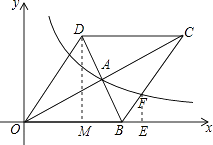
∵点D的坐标为(6,8),
∴OD= ![]() =10,
=10,
∵四边形OBCD是菱形,
∴OB=OD=10,
∴点B的坐标为:(10,0),
∵AB=AD,即A是BD的中点,
∴点A的坐标为:(8,4),
∵点A在反比例函数y= ![]() 上,
上,
∴k=xy=8×4=32,
∵OD∥BC,
∴∠DOM=∠FBE,
∴tan∠FBE=tan∠DOM= ![]() =
= ![]() =
= ![]() ,
,
设EF=4a,BE=3a,
则点F的坐标为:(10+3a,4a),
∵点F在反比例函数y= ![]() 上,
上,
∴4a(10+3a)=32,
即3a2+10a﹣8=0,
解得:a1= ![]() ,a2=﹣4(舍去),
,a2=﹣4(舍去),
∴点F的坐标为:(12, ![]() ).
).
故答案为:(12, ![]() ).
).
首先过点D作DM⊥x轴于点M,过点F作FE⊥x于点E,由点D的坐标为(6,8),可求得菱形OBCD的边长,又由点A是BD的中点,求得点A的坐标,利用待定系数法即可求得反比例函数y= ![]() (x>0)的解析式,然后由tan∠FBE=tan∠DOM=
(x>0)的解析式,然后由tan∠FBE=tan∠DOM= ![]() =
= ![]() =
= ![]() ,可设EF=4a,BE=3a,则点F的坐标为:(10+3a,4a),即可得方程4a(10+3a)=32,继而求得a的值,则可求得答案.
,可设EF=4a,BE=3a,则点F的坐标为:(10+3a,4a),即可得方程4a(10+3a)=32,继而求得a的值,则可求得答案.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=﹣ ![]() +bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣
+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣ ![]() +bx+c的图象分别交于B,C两点,点B在第一象限.
+bx+c的图象分别交于B,C两点,点B在第一象限.
(1)求二次函数y=﹣ ![]() +bx+c的表达式;
+bx+c的表达式;
(2)连接AB,求AB的长;
(3)连接AC,M是线段AC的中点,将点B绕点M旋转180°得到点N,连接AN,CN,判断四边形ABCN的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两点在反比例函数y= ![]() 的图象上,C,D两点在反比例函数y=
的图象上,C,D两点在反比例函数y= ![]() 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1﹣k2的值是( )
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则k1﹣k2的值是( ) 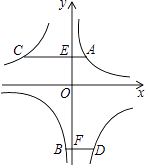
A.6
B.4
C.3
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点M是第一象限内一点,过M的直线分别交x轴,y轴的正半轴于A,B两点,且M是AB的中点.以OM为直径的⊙P分别交x轴,y轴于C,D两点,交直线AB于点E(位于点M右下方),连结DE交OM于点K. 
(1)若点M的坐标为(3,4), ①求A,B两点的坐标;
②求ME的长.
(2)若 ![]() =3,求∠OBA的度数.
=3,求∠OBA的度数.
(3)设tan∠OBA=x(0<x<1), ![]() =y,直接写出y关于x的函数解析式.
=y,直接写出y关于x的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示. 
(1)求甲行走的速度;
(2)在坐标系中,补画s关于t的函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E. 
(1)求证:DE=AB.
(2)以D为圆心,DE为半径作圆弧交AD于点G.若BF=FC=1,试求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABC1D1的边长为1,延长C1D1到A1 , 以A1C1为边向右作正方形A1C1C2D2 , 延长C2D2到A2 , 以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推….若A1C1=2,且点A,D2 , D3 , …,D10都在同一直线上,则正方形A9C9C10D10的边长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE= ![]() AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=
AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF= ![]() :2.当边AD或BC所在的直线与⊙O相切时,AB的长是 .
:2.当边AD或BC所在的直线与⊙O相切时,AB的长是 . 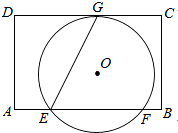
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路. 
(1)求改直的公路AB的长;
(2)问公路改直后比原来缩短了多少千米?(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com