
����Ŀ����������ƽ���ڵĵ㣬�ֽ��õ�����ƽ��1����λ��������ƽ��2�ĵ�λ�����ֵ���˶���Ϊ��A��бƽ�ƣ����P��2��3����1��бƽ�ƺ�ĵ������Ϊ��3��5������֪��A������Ϊ��1��0����
��1���ֱ�д����A��1�Σ�2��бƽ�ƺ�õ��ĵ�����꣮
��2����ͼ����M��ֱ��l�ϵ�һ�㣬��A���ڵ�M�ĶԳƵ�ĵ�B����B����ֱ��l�ĶԳ���Ϊ��C��
����A��B��C���㲻��ͬһ��ֱ���ϣ��жϡ�ABC�Ƿ���ֱ�������Σ���˵�����ɣ�
������B�ɵ�A��n��бƽ�ƺ�õ����ҵ�C������Ϊ��7��6���������B�����꼰n��ֵ��
���𰸡�
��1��
�⣺�ߵ�P��2��3����1��бƽ�ƺ�ĵ������Ϊ��3��5������A������Ϊ��1��0����
���A��1��ƽ�ƺ�õ��ĵ������Ϊ��2��2������A��2��ƽ�ƺ�õ��ĵ�����꣨3��4��
��2��
�⣺������CM����ͼ1��

�����ĶԳƿ�֪��AM=BM��
����Գƿ�֪��BM=CM��
��AM=CM=BM��
���MAC=��ACM����MBC=��MCB��
�ߡ�MAC+��ACM+��MBC+��MCB=180�㣬
���ACM+��MCB=90�㣬
���ACB=90�㣬
���ABC��ֱ�������Σ�
���ӳ�BC��x���ڵ�E����C����CF��AE�ڵ�F����ͼ2��
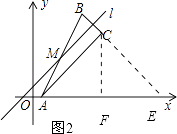
��A��1��0����C��7��6����
��AF=CF=6��
���ACF�ǵ���ֱ�������Σ�
�ɢٵá�ACE=90�㣬
���AEC=45�㣬
��E��������13��0����
��ֱ��BE�Ľ���ʽΪy=kx+b��
��C��E����ֱ���ϣ�
�ɵã� ![]() ��
��
��ã� ![]() ��
��
��y=��x+13��
�ߵ�B�ɵ�A��n��бƽ�Ƶõ���
���B��n+1��2n������2n=��n��1+13��
��ã�n=4��
��B��5��8��
����������1������ƽ�Ƶ����ʵó���Aƽ�Ƶ����꼴�ɣ���2��������CM���������ĺ���ԳƵ����ʺ�ֱ�������ε��ж���ɣ����ӳ�BC��x���ڵ�E����C����CF��AE�ڵ�F�����ݴ���ϵ�����ó�ֱ�ߵĽ���ʽ������ɣ�


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=3ax2+2bx+c
��1����a=b=1��c=��1�����������x��Ľ������ꣻ
��2����a= ![]() ��c=2+b���������ک�2��x��2�����ϵ���Сֵ�ǩ�3����b��ֵ��
��c=2+b���������ک�2��x��2�����ϵ���Сֵ�ǩ�3����b��ֵ��
��3����a+b+c=1���Ƿ����ʵ��x��ʹ����Ӧ��y��ֵΪ1����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=2����DAB=60�㣬��E��AD�ߵ��е㣮��M��AB����һ���㣨�����A�غϣ����ӳ�ME������CD�ڵ�N������MD��AN�� 
��1����֤���ı���AMDN��ƽ���ı��Σ�
��2����գ��ٵ�AM��ֵΪʱ���ı���AMDN�Ǿ��Σ�
�ڵ�AM��ֵΪʱ���ı���AMDN�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���졢�������ֱ�����180ǧ�ļס�������ͬʱ��������ͬһ·��������ʻ��������У��쳵�����ҵ�ͣ��һ��ʱ���ԭ·ԭ�ٷ��ؼأ���������رȿ쳵������� ![]() Сʱ�������ٶ��ǿ쳵�ٶȵ�һ�룬�졢����������غ�ֹͣ��ʻ����������Գ����ص�·��y��ǧ�ף�������ʱ��x��Сʱ���ĺ���ͼ����ͼ��ʾ������ͼ����Ϣ����������⣺
Сʱ�������ٶ��ǿ쳵�ٶȵ�һ�룬�졢����������غ�ֹͣ��ʻ����������Գ����ص�·��y��ǧ�ף�������ʱ��x��Сʱ���ĺ���ͼ����ͼ��ʾ������ͼ����Ϣ����������⣺ 
��1����ֱ��д���졢���������ٶȣ�
��2����쳵���ع�����y��ǧ�ף���x��Сʱ���ĺ�����ϵʽ��
��3�������������ʱ�����90ǧ��·�̣�ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��x�ύ�ڵ�A��1��0������y�ύ�ڵ�B��0����2���� 
��1����ֱ��AB�Ľ���ʽ��
��2����ֱ��AB�ϵĵ�C�ڵ�һ���ޣ���S��BOC=2�����C�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ���˽�ѧ������������������������˲���ѧ��һ�ܲμ�����������ʱ�䣬�õ���ͼ������ͳ��ͼ������ͼ�ν���������⣺ 
��1����γ������ѧ����
��2��������ѧ��һ��ƽ���μ�������������Сʱ��
��3����֪��У��1200��ѧ�������Ƹ�У�ж�����ѧ��һ�ܲμ�����������ʱ�䳬��6Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��45�㣼��A��90�㣬�����и�ʽ�������ǣ� �� 
A.sinA=cosA
B.sinA��cosA
C.sinA��tanA
D.sinA��cosA
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB���O�����ڵ�B��BCΪ��O���ң�OC��OA��OA��BC�ཻ�ڵ�P�� 
��1����֤��AP=AB��
��2����OB=4��AB=3�����߶�BP�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com