
【题目】如图1,P是线段AB上的一点,在AB的同侧作△APC和△BPD,使PC=PA,PD=PB,∠APC=∠BPD,连接CD,点E、F、G、H分别是AC、AB、BD、CD的中点,顺次连接E、F、G、H.
(1)猜想四边形EFGH的形状,直接回答,不必说明理由;
(2)当点P在线段AB的上方时,如图2,在△APB的外部作△APC和△BPD,其他条件不变,(1)中的结论还成立吗?说明理由;
(3)如果(2)中,∠APC=∠BPD=90°,其他条件不变,先补全图3,再判断四边形EFGH的形状,并说明理由.

【答案】(1)四边形EFGH是菱形;
(2)成立,理由见解析;
(3)补全图形见解析;四边形EFGH是正方形,理由见解析.
【解析】试题分析:(1)连接AD、BC,利用SAS可判定△APD≌△CPB,从而得到AD=BC,因为EF、FG、GH、EH分别是△ABC、△ABD、△BCD、△ACD的中位线,则可以得到EF=FG=GH=EH,根据四边都相等的四边形是菱形,可推出四边形EFGH是菱形;(2)成立,可以根据四边都相等的四边形是菱形判定;(3)先将图形补充完整,再通过角之间的关系得到∠EHG=90°,已证四边形EFGH是菱形,则四边形EFGH是正方形.
试题解析:(1)四边形EFGH是菱形.
(2)成立.理由:连接AD,BC.
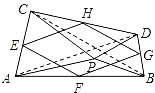
∵∠APC=∠BPD,
∴∠APC+∠CPD=∠BPD+∠CPD.
即∠APD=∠CPB.
又∵PA=PC,PD=PB,
∴△APD≌△CPB(SAS)
∴AD=CB.
∵E、F、G、H分别是AC、AB、BD、CD的中点,
∴EF、FG、GH、EH分别是△ABC、△ABD、△BCD、△ACD的中位线.
∴EF=![]() BC,FG=
BC,FG=![]() AD,GH=
AD,GH=![]() BC,EH=
BC,EH=![]() AD.
AD.
∴EF=FG=GH=EH.
∴四边形EFGH是菱形.
(3)补全图形,如答图.
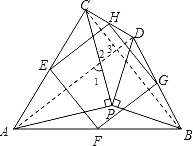
判断四边形EFGH是正方形.
理由:连接AD,BC.
∵(2)中已证△APD≌△CPB.
∴∠PAD=∠PCB.
∵∠APC=90°,
∴∠PAD+∠1=90°.
又∵∠1=∠2.
∴∠PCB+∠2=90°.
∴∠3=90°.
∵(2)中已证GH,EH分别是△BCD,△ACD的中位线,
∴GH∥BC,EH∥AD.
∴∠EHG=90°.
又∵(2)中已证四边形EFGH是菱形,
∴菱形EFGH是正方形.


科目:初中数学 来源: 题型:
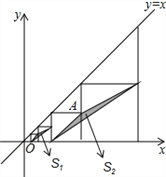
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则Sn的值为__.(用含n的代数式表示,n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京时间2011年3月11日,日本近海发生9.0级强烈地震.本次地震导致地球当天自转快了0.0000016秒.这里的0.0000016秒请你用科学记数法表示为秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.下列结论不一定成立的是【 】

A.△AED≌△BFA B.DE﹣BF=EF C.△BGF∽△DAE D.DE﹣BG=FG
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现给出下列四个命题:
①等边三角形既是轴对称图形,又是中心对称图形;②相似三角形的面积比等于它们的相似比;
③菱形的面积等于两条对角线的积;④三角形的三个内角中至少有一内角不小于60°.
其中不正确的命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标都在格点上,且△A1B1C1与△ABC关于原点O成中心对称,C点坐标为(-2,1)。
(1)请直接写出A1的坐标 ;并画出△A1B1C1.
(2)P(a,b)是△ABC的AC边上一点,将△ABC平移后点P的对称点P'(a+2,b﹣6),请画出平移后的△A2B2C2.
(3)若△A1B1C1和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD= ![]() AM2.
AM2.
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①所有的有理数都能用数轴上的点表示;
②符号不同的两个数互为相反数;
③有理数分为正数和负数;
④两数相减,差一定小于被减数;
⑤两数相加,和一定大于任何一个加数.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com