
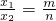 (m≠0,n≠0).
(m≠0,n≠0).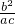 的式子;
的式子;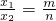 使
使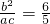 成立?若存在,求出m和n的值;若不存在,请说明理由.
成立?若存在,求出m和n的值;若不存在,请说明理由. ①,x1x2=
①,x1x2= ②.
②. =
= ,得x1=
,得x1= x2③.
x2③. .
. .
.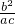 =
= .
. =
= 成立,
成立, ,mn=5k.
,mn=5k. z+5k=0的根.
z+5k=0的根. )2-20k=-14k<0(k>0).
)2-20k=-14k<0(k>0). ①,x1x2=
①,x1x2= ②,由已知
②,由已知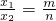 变形后代入①②,联立方程,消去x,就可得到
变形后代入①②,联立方程,消去x,就可得到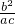 值.
值. =
= 成立,设出适当的参数,建立关于以m+n和mn为两根的新的一元二次方程,求得其△的符号后,来判定根的情况后,决定是否存在m,n的值.
成立,设出适当的参数,建立关于以m+n和mn为两根的新的一元二次方程,求得其△的符号后,来判定根的情况后,决定是否存在m,n的值. ;
; .
. 

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
A、
| ||||
B、
| ||||
C、±
| ||||
D、±
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com