
科目:初中数学 来源: 题型:填空题
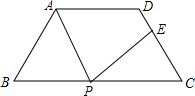 如图,在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=14cm,∠B=60°,P为下底BC上一点(不与点B、C重合),连接AP,过点P作射线PE交线段DC于点E,使得∠APE=∠B,若DE:EC=5:3,则BP=2cm或12cm.
如图,在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=14cm,∠B=60°,P为下底BC上一点(不与点B、C重合),连接AP,过点P作射线PE交线段DC于点E,使得∠APE=∠B,若DE:EC=5:3,则BP=2cm或12cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
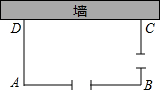 矩形自行车场地ABCD一边靠墙(墙长10m),在AB和BC边各开一个1米宽的校门(不用木板),现有能围成14m长的木板,当AD长为多少时,自行车场地的面积最大?最大面积是多少.
矩形自行车场地ABCD一边靠墙(墙长10m),在AB和BC边各开一个1米宽的校门(不用木板),现有能围成14m长的木板,当AD长为多少时,自行车场地的面积最大?最大面积是多少.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com