
ЁОЬтФПЁПКажагаШєИЩУЖКкЦхКЭАзЦхЃЌетаЉЦхГ§беЩЋЭтЮоЦфЫћВюБ№ЃЌЯжШУбЇЩњНјааУўЦхЪдбщЃКУПДЮУўГівЛУЖЦхЃЌМЧТМбеЩЋКѓЗХЛивЁдШЃЎжиИДНјааетбљЕФЪдбщЕУЕНвдЯТЪ§ОнЃК
УўЦхЕФДЮЪ§n | 100 | 200 | 300 | 500 | 800 | 1000 |
УўЕНКкЦхЕФДЮЪ§m | 24 | 51 | 76 | 124 | 201 | 250 |
УўЕНКкЦхЕФЦЕТЪ | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
ЃЈ1ЃЉИљОнБэжаЪ§ОнЙРМЦДгКажаУўГівЛУЖЦхЪЧКкЦхЕФИХТЪЪЧЁЁ ЁЁЃЛЃЈОЋШЗЕН0.01ЃЉ
ЃЈ2ЃЉШєКажаКкЦхгыАзЦхЙВга4УЖЃЌФГЭЌбЇвЛДЮУўГіСНУЖЦхЃЌЧыМЦЫуетСНУЖЦхбеЩЋВЛЭЌЕФИХТЪЃЌВЂЫЕУїРэгЩ
ЁОД№АИЁПЃЈ1ЃЉ0.25ЃЛЃЈ2ЃЉ![]() .
.
ЁОНтЮіЁП
![]() ДѓСПжиИДЪдбщЯТУўЧђЕФЦЕТЪПЩвдЙРМЦУўЧђЕФИХТЪ;
ДѓСПжиИДЪдбщЯТУўЧђЕФЦЕТЪПЩвдЙРМЦУўЧђЕФИХТЪ;
![]() ЛЪїзДЭМСаГіЫљгаЕШПЩФмНсЙћЃЌдйевЕНЗћКЯЬѕМўЕФНсЙћЪ§ЃЌИљОнИХТЪЙЋЪНЧѓНт.
ЛЪїзДЭМСаГіЫљгаЕШПЩФмНсЙћЃЌдйевЕНЗћКЯЬѕМўЕФНсЙћЪ§ЃЌИљОнИХТЪЙЋЪНЧѓНт.
ЃЈ1ЃЉИљОнБэжаЪ§ОнЙРМЦДгКажаУўГівЛУЖЦхЪЧКкЦхЕФИХТЪЪЧ0.25ЃЌ
ЙЪД№АИЮЊЃК0.25ЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉПЩжЊЃЌКкЦхЕФИіЪ§ЮЊ4ЁС0.25=1ЃЌдђАзЦхзгЕФИіЪ§ЮЊ3ЃЌ
ЛЪїзДЭМШчЯТЃК
гЩБэПЩжЊЃЌЫљгаЕШПЩФмНсЙћЙВга12жжЧщПіЃЌ
ЦфжаетСНУЖЦхбеЩЋВЛЭЌЕФга6жжНсЙћЃЌ
ЫљвдетСНУЖЦхбеЩЋВЛЭЌЕФИХТЪЮЊ![]() ЃЎ
ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГХњЗЂГЧдкЖЌЬьЕНРДжЎМЪНјСЫвЛХњБЃХЏвТЃЌФаЩњЕФБЃХЏвТУПМўМлИё60дЊЃЌХЎЩњЕФБЃХЏвТУПМўМлИё40дЊЃЌЕквЛХњЙВЙКТђ100МўЃЎ
ЃЈ1ЃЉЕквЛХњЙКТђЕФБЃХЏвТЕФзмЗбгУВЛГЌЙ§5400дЊЃЌЧѓХЎЩњБЃХЏвТзюЩйЙКТђЖрЩйМўЃП
ЃЈ2ЃЉЕкЖўХњЙКТђБЃХЏвТЃЌЙКТђФаЁЂХЎЩњБЃХЏвТЕФМўЪ§БШЮЊ![]() ЃЌМлИёБЃГжЕквЛХњЕФМлИёВЛБфЃЛЕкШ§ХњЙКТђФаЩњБЃХЏвТЕФМлИёдкЕквЛХњЙКТђЕФМлИёЩЯУПМўМѕЩйСЫ
ЃЌМлИёБЃГжЕквЛХњЕФМлИёВЛБфЃЛЕкШ§ХњЙКТђФаЩњБЃХЏвТЕФМлИёдкЕквЛХњЙКТђЕФМлИёЩЯУПМўМѕЩйСЫ![]() дЊ ЃЌХЎЩњБЃХЏвТЕФМлИёБШЕквЛХњЙКТђЕФМлИёЩЯУПМўдіМгСЫ
дЊ ЃЌХЎЩњБЃХЏвТЕФМлИёБШЕквЛХњЙКТђЕФМлИёЩЯУПМўдіМгСЫ![]() дЊЃЌФаЩњБЃХЏвТЕФЪ§СПБШЕкЖўХњдіМгСЫ
дЊЃЌФаЩњБЃХЏвТЕФЪ§СПБШЕкЖўХњдіМгСЫ![]() ЃЌХЎЩњБЃХЏвТЕФЪ§СПБШЕкЖўХњМѕЩйСЫ
ЃЌХЎЩњБЃХЏвТЕФЪ§СПБШЕкЖўХњМѕЩйСЫ![]() ЃЌЕкЖўХњгыЕкШ§ХњЙКТђБЃХЏвТЕФзмЗбгУЯрЭЌЃЌЧѓ
ЃЌЕкЖўХњгыЕкШ§ХњЙКТђБЃХЏвТЕФзмЗбгУЯрЭЌЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
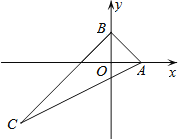
ЁОЬтФПЁПШчЭМЃЌЁїABCдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЁЂBЗжБ№дкxжсКЭyжсЩЯЃЌЧвOAЃНOBЃЌБпACЫљдкжБЯпНтЮіЪНЮЊyЃН![]() xЉ
xЉ![]() ЃЌШєЁїABCЕФФкаФдкyжсЩЯЃЌдђtanЁЯACBЕФжЕЮЊЃЈЁЁЁЁЃЉ
ЃЌШєЁїABCЕФФкаФдкyжсЩЯЃЌдђtanЁЯACBЕФжЕЮЊЃЈЁЁЁЁЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌБпГЄЮЊ1ЕФе§ЗНаЮABCDЕФЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЎгажБНЧЁЯMPNЃЌЪЙжБНЧЖЅЕуPгыЕуOжиКЯЃЌжБНЧБпPMЁЂPNЗжБ№гыOAЁЂOBжиКЯЃЌШЛКѓФцЪБеыа§зЊЁЯMPNЃЌа§зЊНЧЮЊІШЃЈ0ЁуЃМІШЃМ90ЁуЃЉЃЌPMЁЂPNЗжБ№НЛABЁЂBCгкEЁЂFСНЕуЃЌСЌНгEFНЛOBгкЕуGЃЌдђЯТСаНсТлжае§ШЗЕФЪЧ ЃЎ
ЃЈ1ЃЉEF=![]() OEЃЛЃЈ2ЃЉSЫФБпаЮOEBFЃКSе§ЗНаЮABCD=1ЃК4ЃЛЃЈ3ЃЉBE+BF=
OEЃЛЃЈ2ЃЉSЫФБпаЮOEBFЃКSе§ЗНаЮABCD=1ЃК4ЃЛЃЈ3ЃЉBE+BF=![]() OAЃЛЃЈ4ЃЉдка§зЊЙ§ГЬжаЃЌЕБЁїBEFгыЁїCOFЕФУцЛ§жЎКЭзюДѓЪБЃЌAE=
OAЃЛЃЈ4ЃЉдка§зЊЙ§ГЬжаЃЌЕБЁїBEFгыЁїCOFЕФУцЛ§жЎКЭзюДѓЪБЃЌAE=![]() ЃЛЃЈ5ЃЉOGBD=AE2+CF2ЃЎ
ЃЛЃЈ5ЃЉOGBD=AE2+CF2ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
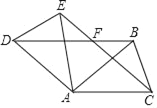
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЃЌABЃНACЃЌАбЁїABCШЦAЕуЫГЪБеыЗНЯђа§зЊЕУЕНЁїADEЃЌСЌНгBDЃЌCEНЛгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAECЁеЁїADBЃЛ
ЃЈ2ЃЉШєABЃН![]() ЃЌЁЯBACЃН45ЁуЃЌЕБЫФБпаЮADFCЪЧСтаЮЪБЃЌЧѓBFЕФГЄЃЎ
ЃЌЁЯBACЃН45ЁуЃЌЕБЫФБпаЮADFCЪЧСтаЮЪБЃЌЧѓBFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпy=ax2+bx+c ШчЭМЫљЪОЃЌжБЯпx=-1ЪЧЦфЖдГЦжсЃЌ

ЃЈ1ЃЉШЗЖЈaЃЌbЃЌcЃЌ ІЄ=b2-4acЕФЗћКХЃЌ
ЃЈ2ЃЉЧѓжЄЃКa-b+c>0ЃЌ
ЃЈ3ЃЉЕБxШЁКЮжЕЪБЃЌy>0ЃЛЕБxШЁКЮжЕЪБy<0.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГХЉзїЮяЕФЩњГЄТЪPгыЮТЖШt(Ёц)гаШчЯТЙиЯЕЃКШчЭМ1ЃЌЕБ10ЁмtЁм25ЪБПЩНќЫЦгУКЏЪ§![]() ПЬЛЃЛЕБ25ЁмtЁм37ЪБПЩНќЫЦгУКЏЪ§
ПЬЛЃЛЕБ25ЁмtЁм37ЪБПЩНќЫЦгУКЏЪ§![]() ПЬЛЃЎ
ПЬЛЃЎ
(1)ЧѓhЕФжЕЃЎ
(2)АДееОбщЃЌИУзїЮяЬсЧАЩЯЪаЕФЬьЪ§m(Ьь)гыЩњГЄТЪPТњзуКЏЪ§ЙиЯЕЃК
ЩњГЄТЪP | 0.2 | 0.25 | 0.3 | 0.35 |
ЬсЧАЩЯЪаЕФЬьЪ§mЃЈЬьЃЉ | 0 | 5 | 10 | 15 |
ЂйЧыдЫгУвббЇЕФжЊЪЖЃЌЧѓmЙигкPЕФКЏЪ§БэДяЪНЃЛ
ЂкЧыгУКЌ![]() ЕФДњЪ§ЪНБэЪОm ЃЛ
ЕФДњЪ§ЪНБэЪОm ЃЛ
(3)ЬьЦјКЎРфЃЌДѓХяМгЮТПЩИФБфХЉзїЮяЩњГЄЫйЖШЃЎдк(2)ЕФЬѕМўЯТЃЌдМЦЛЎДѓХяКуЮТ20ЁцЪБЃЌУПЬьЕФГЩБОЮЊ200дЊЃЌИУзїЮя30ЬьКѓЩЯЪаЪБЃЌИљОнЪаГЁЕїВщЃКУПЬсЧАвЛЬьЩЯЪаЪлГі(вЛДЮЪлЭъ)ЃЌЯњЪлЖюПЩдіМг600дЊЃЎвђДЫИјДѓХяМЬајМгЮТЃЌМгЮТКѓУПЬьГЩБОw(дЊ)гыДѓХяЮТЖШt(Ёц)жЎМфЕФЙиЯЕШчЭМ2ЃЎЮЪЬсЧАЩЯЪаЖрЩйЬьЪБдіМгЕФРћШѓзюДѓЃПВЂЧѓетИізюДѓРћШѓЃЈХЉзїЮяЩЯЪаЪлГіКѓДѓХяднЭЃЪЙгУЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
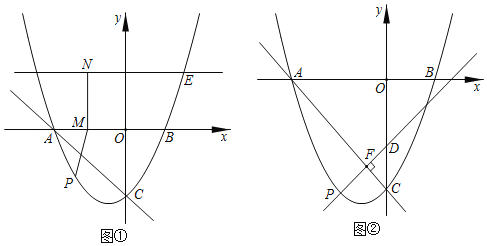
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃН![]() x2+xЉ4гыxжсНЛгкAЃЌBЃЈAдкBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌХзЮяЯпЩЯЕФЕуEЕФКсзјБъЮЊ3ЃЌЙ§ЕуEзїжБЯпl1ЁЮxжсЃЎ
x2+xЉ4гыxжсНЛгкAЃЌBЃЈAдкBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌХзЮяЯпЩЯЕФЕуEЕФКсзјБъЮЊ3ЃЌЙ§ЕуEзїжБЯпl1ЁЮxжсЃЎ
ЃЈ1ЃЉЕуPЮЊХзЮяЯпЩЯЕФЖЏЕуЃЌЧвдкжБЯпACЕФЯТЗНЃЌЕуMЃЌNЗжБ№ЮЊxжсЃЌжБЯпl1ЩЯЕФЖЏЕуЃЌЧвMNЁЭxжсЃЌЕБЁїAPCУцЛ§зюДѓЪБЃЌЧѓPM+MN+![]() ENЕФзюаЁжЕЃЛ
ENЕФзюаЁжЕЃЛ
ЃЈ2ЃЉЙ§ЃЈ1ЃЉжаЕФЕуPзїPDЁЭACЃЌДЙзуЮЊFЃЌЧвжБЯпPDгыyжсНЛгкЕуDЃЌАбЁїDFCШЦЖЅЕуFа§зЊ45ЁуЃЌЕУЕНЁїD'FC'ЃЌдйАбЁїD'FC'бижБЯпPDЦНвЦжСЁїDЁхFЁфCЁхЃЌдкЦНУцЩЯЪЧЗёДцдкЕуKЃЌЪЙЕУвдOЃЌCЁхЃЌDЁхЃЌKЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃПШєДцдкжБНгаДГіЕуKЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃПЊеЙСЫЮЊЦквЛжмЕФЁАОДРЯАЎЧзЁБЩчЛсЛюЖЏЃЌЮЊСЫНтЧщПіЃЌбЇЩњЛсЫцЛњЕїВщСЫВПЗжбЇЩњдкетДЮЛюЖЏжазіМвЮёЕФЪБМфЃЌВЂНЋЭГМЦЕФЪБМфЃЈЕЅЮЛЃКаЁЪБЃЉЗжГЩ5зщЃЌAЃК0.5ЁмxЃМ1ЃЌBЃК1ЁмxЃМ1.5ЃЌCЃК1.5ЁмxЃМ2ЃЌDЃК2ЁмxЃМ2.5ЃЌEЃК2.5ЁмxЃМ3ЃЌжЦзїГЩСНЗљВЛЭъећЕФЭГМЦЭМЃЈШчЭМЃЉЃЎ

ЧыИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉбЇЩњЛсЫцЛњЕїВщСЫЁЁ ЁЁУћбЇЩњЃЛ
ЃЈ2ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉШєШЋаЃга900УћбЇЩњЃЌЙРМЦИУаЃдкетДЮЛюЖЏжазіМвЮёЕФЪБМфВЛЩйгк2.5аЁЪБЕФбЇЩњгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com