
����Ŀ��ij�������ڶ��쵽��֮�ʽ���һ����ů�£������ı�ů��ÿ���۸�60Ԫ��Ů���ı�ů��ÿ���۸�40Ԫ����һ��������100����
��1����һ������ı�ů�µ��ܷ��ò�����5400Ԫ����Ů����ů�����ٹ�����ټ���
��2���ڶ�������ů�£������С�Ů����ů�µļ�����Ϊ![]() ���۸ֵ�һ���ļ۸䣻����������������ů�µļ۸��ڵ�һ������ļ۸���ÿ��������
���۸ֵ�һ���ļ۸䣻����������������ů�µļ۸��ڵ�һ������ļ۸���ÿ��������![]() Ԫ ��Ů����ů�µļ۸�ȵ�һ������ļ۸���ÿ��������
Ԫ ��Ů����ů�µļ۸�ȵ�һ������ļ۸���ÿ��������![]() Ԫ��������ů�µ������ȵڶ���������
Ԫ��������ů�µ������ȵڶ���������![]() ��Ů����ů�µ������ȵڶ���������
��Ů����ů�µ������ȵڶ���������![]() ���ڶ��������������ů�µ��ܷ�����ͬ����
���ڶ��������������ů�µ��ܷ�����ͬ����![]() ��ֵ��
��ֵ��
���𰸡���1��Ů����ů�����ٹ�30������2��![]() ��ֵ��
��ֵ��![]()
��������
��1����Ů����ů�¹���x�������������в���ʽ��ɣ�
��2���蹺���С�Ů����ů�µļ����ֱ�Ϊ![]() �����������з��̽ⷽ�̼��ɵõ���.
�����������з��̽ⷽ�̼��ɵõ���.
��1����Ů����ů�¹���x����
40x��60��100��x����5400
��֮��x��30
��Ů����ů�����ٹ�30��
��2���蹺���С�Ů����ů�µļ����ֱ�Ϊ![]() ��
��
�������⣬��
![]()
��m%=t����m=100t��
![]()
![]()
![]() ����ȥ����
����ȥ����![]()
��m=100t=![]() ��
��
��![]() ��ֵ��
��ֵ��![]() .
.


 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+3x+1��m=0����������ȵ�ʵ������
��1����m��ȡֵ��Χ��
��2����mΪ�����������ʱ���̵ĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
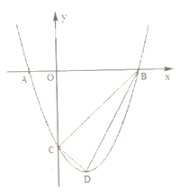
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��������
��������![]() ������
������![]() ��
��![]() .
.

��1�����B������������ߵĽ���ʽ��
��2��M��m��0��Ϊx����һ�����㣬����M��ֱ��x���ֱ����ֱ��AB�������߷ֱ��ڵ�P��N��
����![]() ���߶�
���߶�![]() ���˶�������
���˶�������![]() ��
��![]() ��
��![]() �������������
Ϊ�������������![]() ���ƣ����
���ƣ����![]() �����ꣻ
�����ꣻ
����![]() ��
��![]() ���������˶�����������
���������˶�����������![]() ��
��![]() ��
��![]() ��ǡ��һ�����������������߶ε��е㣨�����غϳ��⣩�����
��ǡ��һ�����������������߶ε��е㣨�����غϳ��⣩�����![]() ��
��![]() ��
��![]() ����Ϊ����г����.��ֱ��д��ʹ��
����Ϊ����г����.��ֱ��д��ʹ��![]() ��
��![]() ��
��![]() �����Ϊ����г������
�����Ϊ����г������![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У�AB��AC����ABC����������A��ֱ��MN��ʹMN��BC����D��ֱ��MN�ϣ�������BD��������BD�Ƶ�B˳ʱ����ת������ֱ��AC�ڵ�E��
��1����ͼ�٣�������60�����ҵ�D������AN��ʱ��ֱ��д���߶�AB��AD��AE��������ϵ��
��2����ͼ�ڣ�������45�����ҵ�D������AN��ʱ��ֱд���߶�AB��AD��AE��������ϵ����˵�����ɣ�
��3��������30��ʱ������D������AM�ϣ���ABE��15����AD��![]() ��1����ֱ��д���߶�AE�ij��ȣ�
��1����ֱ��д���߶�AE�ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ���ύ��
���ύ��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ���������ߵĶ���Ϊ��
���������ߵĶ���Ϊ��![]() ��
��
��1����������ߵĽ���ʽ�붥��![]() �����꣮
�����꣮
��2�����ж�![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
��3�����������Ƿ���ڵ�![]() ��ʹ����
��ʹ����![]() Ϊ�������������
Ϊ�������������![]() ���ƣ������ڣ���ֱ��д����
���ƣ������ڣ���ֱ��д����![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
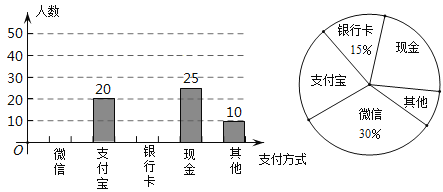
����Ŀ���й�������֧����������δ�������֧����ʽ���й������ߵ��ƶ�֧�����������ƶ�֧��Ҫ���11�������Ե�����չ������Ǯ����δ��ʱ���й���һ����Ȼ����㣮ijУ��ѧ��ȤС�������һ�ݵ����ʾ���Ҫ��ÿ��ѡ��ֻѡһ������ϲ����֧����ʽ���ֽ�����������ͳ�Ʋ����Ƴ�����������������ͳ��ͼ������ͼ����������Ϣ����������⣺
��1����λ���������� ���ˣ�������ͳ��ͼ�У���ʾ��֧������֧��������Բ�ĽǵĶ���Ϊ�� ����
��2��������ͳ��ͼ�����������۲��ͼ��������֧����ʽ�����������һ�����ݣ����������ݵ�����λ���������� ������
��3����һ�ι����У�С����С�����������������֧�������������п�������֧����ʽ��ѡһ�ַ�ʽ����֧�������û���״ͼ���б���ķ�����������ѡͬ��֧����ʽ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ڿ�ѧ����880Ԫ�������ɸ�ѧ��ר�ÿ�ѧ����������ÿ��50Ԫ���ۣ��ܿ������һ�գ����˽�ѧ��������3�����ּ���������������2580Ԫ�����������������������ÿ�����۱��ϴ��Ż�1Ԫ���õ���ÿ��50Ԫ���ۣ����ʣ��4���������������������õ깲ӯ���� ��Ԫ��
A��508 B��520 C��528 D��560
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
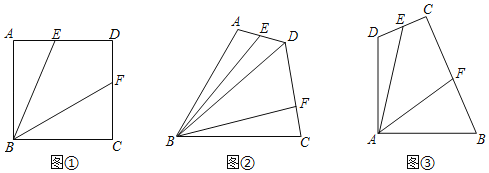
����Ŀ��������⣺��1����ͼ�٣�������ABCD�У���E����F�ֱ��ڱ�AD�ͱ�CD�ϣ��������α߳�Ϊ4��DE+DF��4�����ı���BEDF�����Ϊ�� ��
̽�����⣺��2����ͼ�ڣ��ı���ABCD��AB��BC��4����ABC��60������ADC��120������E��F�ֱ��DZ�AD�ͱ�DC�ϵĵ㣬����BE��BF����ED+DF��3��BD��2![]() �����ı���EBFD�������
�����ı���EBFD�������
������⣺��3��ij���ʿ�̽��Ϊ�˽�����Դ���⣬��������ͼ����ʾ��һ���ı���Ұ�⿱����أ�������������߽�DA��AB���Ⱦ�Ϊ4km����DAB��90�������ڿ�����Ҫ������ԭ����������C����ر�ԵD��B�н�Ϊ90������DCB��90�������ڱ߽�CD�ͱ߽�BC�Ϸֱ�����������������E��F������������E��F����������C�ľ���֮��ʼ�յ���4km��CE+CF��4����Ϊ�˴ﵽ���ü��Ч�����豣֤���������ı���EAFC����������ܴ����ʿ������������û�����ֵ�������������ֵ�����û�У���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ö����Ͱ��壬��Щ�����ɫ���������������ѧ�������������飺ÿ������һö�壬��¼��ɫ��Ż�ҡ�ȣ��ظ���������������õ��������ݣ�
����Ĵ���n | 100 | 200 | 300 | 500 | 800 | 1000 |
��������Ĵ���m | 24 | 51 | 76 | 124 | 201 | 250 |
���������Ƶ�� | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
��1�����ݱ������ݹ��ƴӺ�������һö���Ǻ���ĸ������� ��������ȷ��0.01��
��2�������к�������干��4ö��ijͬѧһ��������ö�壬���������ö����ɫ��ͬ�ĸ��ʣ���˵������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com