
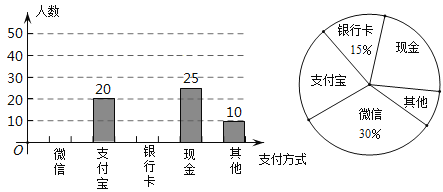
【题目】中国的数字支付正在引领未来世界的支付方式变革,中国消费者的移动支付比美国的移动支付要多出11倍,所以当我们展望数字钱包的未来时,中国是一个自然的起点.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,将各种支付方式调查人数组成一组数据,求这组数据的“中位数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求两人选同种支付方式的概率.
【答案】(1)100、72°;(2)图详见解析,20;(3)![]() .
.
【解析】
(1)根据已知的支付宝、现金及其他的人数和除以这三部分的额百分比即可得到总人数,再利用“支付宝”支付的人数除以总人数乘以360°即可得到“支付宝”支付的圆心角的度数;
(2)利用总人数及百分比求出微信及银行卡支付的人数,由此补全条形图,根据5种支付方式的人数即可得到中位数;
(3)列树状图即可解答.
解:(1)本次活动调查的总人数为(20+25+10)÷(1﹣15%﹣30%)=100人,
则表示“支付宝”支付的扇形圆心角的度数为360°×![]() =72°,
=72°,
故答案为:100、72°;
(2)微信人数为100×30%=30人,银行卡人数为100×15%=15人,
补全图形如下:

由条形图知,这组数据的5个数据重新排列为:10、15、20、25、30,故中位数是20,
故答案为:20;
(3)将微信记为A、支付宝记为B、银行卡记为C,
画树状图得:
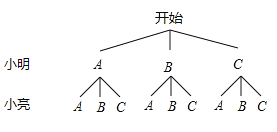
∵由树状图知,共有9种等可能的结果,其中两人选用同一种支付方式的有3种,
∴P(两人选用同种支付方式)=![]() .
.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
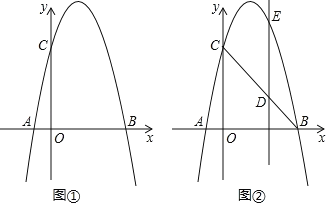
【题目】如图①,抛物线y=﹣x2+bx+c与x轴交于点A和点B(4,0),与y轴交于点C(0,4).
(1)求出抛物线的函数表达式.
(2)抛物线上是否存在一点P,使得S△OBC=4S△AOP,若存在求出点P的坐标;若不存在,请说明理由.
(3)如图②,点D为线段BC上一动点,过点D作DE∥y轴交抛物线于点E,求线段DE长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着城际铁路的开通,从甲市到乙市的高铁里程比快里程缩短了90千米,运行时间减少了8小时,已知甲市到乙市的普快列车里程为1220千米,高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)若从甲市到乙市途经丙市,且从甲市到丙市的高铁里程为780千米.某日王老师要从甲市去丙市参加14:00召开的会议,如果他买了当日10:00从甲市到丙市的高铁票,而且从丙市高铁站到会议地点最多需要0.5小时.试问在高铁列车准点到达的情况下,王老师能否在开会之前赶到会议地点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 购买江苏省体育彩票有“中奖”与“不中奖”两种情况,所以中奖的概率是![]()
B. 国家级射击运动员射靶一次,正中靶心是必然事件
C. 如果在若干次试验中一个事件发生的频率是![]() ,那么这个事件发生的概率一定也是
,那么这个事件发生的概率一定也是![]()
D. 如果车间生产的零件不合格的概率为![]() ,那么平均每检查1000个零件会查到1个次品
,那么平均每检查1000个零件会查到1个次品
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发城在冬天到来之际进了一批保暖衣,男生的保暖衣每件价格60元,女生的保暖衣每件价格40元,第一批共购买100件.
(1)第一批购买的保暖衣的总费用不超过5400元,求女生保暖衣最少购买多少件?
(2)第二批购买保暖衣,购买男、女生保暖衣的件数比为![]() ,价格保持第一批的价格不变;第三批购买男生保暖衣的价格在第一批购买的价格上每件减少了
,价格保持第一批的价格不变;第三批购买男生保暖衣的价格在第一批购买的价格上每件减少了![]() 元 ,女生保暖衣的价格比第一批购买的价格上每件增加了
元 ,女生保暖衣的价格比第一批购买的价格上每件增加了![]() 元,男生保暖衣的数量比第二批增加了
元,男生保暖衣的数量比第二批增加了![]() ,女生保暖衣的数量比第二批减少了
,女生保暖衣的数量比第二批减少了![]() ,第二批与第三批购买保暖衣的总费用相同,求
,第二批与第三批购买保暖衣的总费用相同,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.
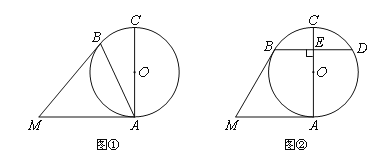
(Ⅰ)如图①,若∠BAC=250,求∠AMB的大小;
(Ⅱ)如图②,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直径为10的⊙O经过原点O,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长分别是方程x2+kx+48=0的两根.

(1)求线段OA、OB的长;
(2)已知点C在劣弧OA上,连结BC交OA于D,当OC2=CD·CB时,求C点的坐标;
(3)在⊙O上是否存在点P,使S△POD=S△ABD.若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
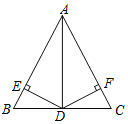
【题目】在△ABC中,AB=AC,点D为边BC上一点,且AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F.
(1)求证:BE=CF;
(2)若∠B=40°,求∠ADF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c 如图所示,直线x=-1是其对称轴,

(1)确定a,b,c, Δ=b2-4ac的符号,
(2)求证:a-b+c>0,
(3)当x取何值时,y>0;当x取何值时y<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com