
【题目】如图①,抛物线y=﹣x2+bx+c与x轴交于点A和点B(4,0),与y轴交于点C(0,4).
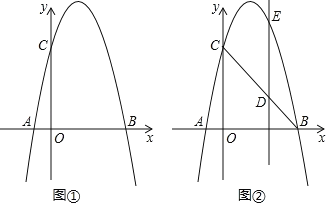
(1)求出抛物线的函数表达式.
(2)抛物线上是否存在一点P,使得S△OBC=4S△AOP,若存在求出点P的坐标;若不存在,请说明理由.
(3)如图②,点D为线段BC上一动点,过点D作DE∥y轴交抛物线于点E,求线段DE长度的最大值.
【答案】(1)y=﹣x2+3x+4;(2)点P坐标(0,4)或(3,4),或(![]() ,﹣4)或(
,﹣4)或(![]() ,﹣4);(3)DE的最大值为4.
,﹣4);(3)DE的最大值为4.
【解析】
(1)利用待定系数法将点B,C代入即可求出抛物线的表达式;
(2)先利用抛物线的表达式求出点A的坐标,进而可求出OA,OB,OC的长度,然后利用面积之间的关系求出点P的纵坐标,再将P的纵坐标代入抛物线的表达式中求出横坐标即可;
(3)先用待定系数法求出直线BC的解析式,然后表示出先对DE的长度,再利用二次函数的性质求最大值即可.
(1)∵抛物线y=﹣x2+bx+c与x轴交于点A和点B(4,0),与y轴交于点C(0,4),
∴![]() ,
,
∴![]() ,
,
∴抛物线解析式为:y=﹣x2+3x+4;
(2)∵y=﹣x2+3x+4与x轴交于点A和点B(4,0),
∴0=﹣x2+3x+4,
∴x1=4,x2=﹣1,
∴点A(﹣1,0),且点B(4,0),点C(0,4),
∴AO=1,BO=CO=4,
设点P(x,y)
∵S△OBC=4S△AOP,
∴![]() OB×OC=4
OB×OC=4![]() AO×|y|,
AO×|y|,
∴|y|=4,
∴y=±4,
当y=4时,4=﹣x2+3x+4,
∴x1=0,x2=3,
∴点P坐标(0,4)或(3,4),
当y=﹣4时,﹣4=﹣x2+3x+4,
∴x3![]() ,x4
,x4![]() ,
,
∴点P坐标(![]() ,﹣4)或(
,﹣4)或(![]() ,﹣4),
,﹣4),
综上所述,点P的坐标为(0,4)或(3,4) 或(![]() ,﹣4)或(
,﹣4)或(![]() ,﹣4)
,﹣4)
(3)设直线BC的解析式为![]()
将点B(4,0), C(0,4)代入解析式中得,
![]() 解得
解得![]()
∴直线BC解析式为:y=﹣x+4,
设点E(a,﹣a2+3a+4),则点D(a,﹣a+4),
∴DE=﹣a2+3a+4﹣(﹣a+4)=﹣(a﹣2)2+4,
当a=2时,DE的最大值为4.


科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 为常数,且
为常数,且![]() )中的
)中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
以下结论:
①二次函数![]() 有最小值为
有最小值为![]() ;
;
②当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
③二次函数![]() 的图象与
的图象与![]() 轴只有一个交点;
轴只有一个交点;
④当![]() 时,
时,![]() .
.
其中正确的结论有( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
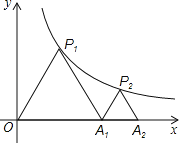
【题目】如图,P1是反比例函数![]() (k>0)在第一象限图象上的一点,点A1的坐标为(2,0).若△P1OA1与△P2A1A2均为等边三角形,则A2点的坐标为_____.
(k>0)在第一象限图象上的一点,点A1的坐标为(2,0).若△P1OA1与△P2A1A2均为等边三角形,则A2点的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=![]() cm.
cm.
(1)求证:AC是⊙O的切线;
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在清江河污水网管改造建设中,需要确保在汛期来临前将建设过程中产生的渣土清运完毕,每天至少需要清运渣土12720m3,施工方准备每天租用大、小两种运输车共80辆.已知每辆大车每天运送渣土200m3,每辆小车每天运送渣土120m3,大、小车每天每辆租车费用分别为1200元,900元,且要求每天租车的总费用不超过85300元.
(1)施工方共有多少种租车方案?
(2)哪种租车方案费用最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司2017年初刚成立时投资1000万元购买新生产线生产新产品,此外,生产每件该产品还需要成本40元.按规定,该产品售价不得低于60元/件且不超过160元/件,且每年售价确定以后不再变化,该产品的年销售量![]() (万件)与产品售价
(万件)与产品售价![]() (元)之间的函数关系如图所示.
(元)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出
之间的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)求2017年该公司的最大利润?
(3)在2017年取得最大利润的前提下,2018年公司将重新确定产品售价,能否使两年共盈利达980万元.若能,求出2018年产品的售价;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
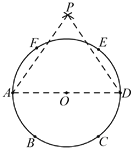
【题目】已知点A、B、C、D、E、F是半径为r的⊙O的六等分点,分别以A、D为圆心,AE和DF长为半径画圆弧交于点P.以下说法正确的是( )
①∠PAD=∠PDA=60; ②△PAO≌△ADE;③PO=![]() r;④AO∶OP∶PA=1∶
r;④AO∶OP∶PA=1∶![]() ∶
∶![]() .
.
A. ①④B. ②③C. ③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
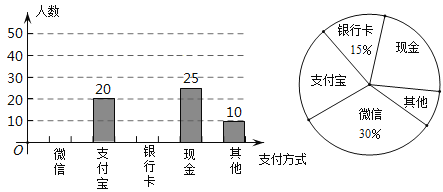
【题目】中国的数字支付正在引领未来世界的支付方式变革,中国消费者的移动支付比美国的移动支付要多出11倍,所以当我们展望数字钱包的未来时,中国是一个自然的起点.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,将各种支付方式调查人数组成一组数据,求这组数据的“中位数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求两人选同种支付方式的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com