
【题目】已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.
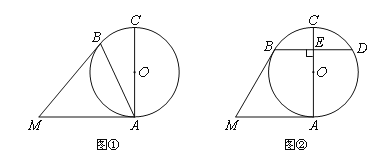
(Ⅰ)如图①,若∠BAC=250,求∠AMB的大小;
(Ⅱ)如图②,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
【答案】(Ⅰ)50°(Ⅱ)60°
【解析】解:(Ⅰ)∵MA切⊙O于点A,∴∠MAC=90°。
又∠BAC=25°,∴∠MAB=∠MAC-∠BAC=65°。
∵MA、MB分别切⊙O于点A、B,∴MA=MB。
∴∠MAB=∠MBA。
∴∠AMB=180°-(∠MAB+∠MBA)=50°。
(Ⅱ)如图,连接AD、AB,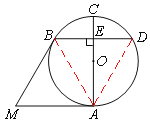
∵MA⊥AC,又BD⊥AC,
∴BD∥MA。
又∵BD=MA,∴四边形MADB是平行四边形。
又∵MA=MB,∴四边形MADB是菱形。∴AD=BD。
又∵AC为直径,AC⊥BD,
∴ AB = AD 。
∴AB=AD=BD。∴△ABD是等边三角形。∴∠D=60°。
∴在菱形MADB中,∠AMB=∠D=60°
(Ⅰ)由AM与圆O相切,根据切线的性质得到AM垂直于AC,可得出∠MAC为直角,再由∠BAC的度数,用∠MAC-∠BAC求出∠MAB的度数,又MA,MB为圆O的切线,根据切线长定理得到MA=MB,利用等边对等角可得出∠MAB=∠MBA,由底角的度数,利用三角形的内角和定理即可求出∠AMB的度数。
(Ⅱ)连接AB,AD,由直径AC垂直于弦BD,根据垂径定理得到A为优弧BAD 的中点,根据等弧对等弦可得出AB=AD,由AM为圆O的切线,得到AM垂直于AC,又BD垂直于AC,根据垂直于同一条直线的两直线平行可得出BD平行于AM,又BD=AM,利用一组对边平行且相等的四边形为平行四边形得到ADBM为平行四边形,再由邻边MA=MB,得到ADBM为菱形,根据菱形的邻边相等可得出BD=AD,进而得到AB=AD=BD,即△ABD为等边三角形,根据等边三角形的性质得到∠D为60°,再利用菱形的对角相等可得出∠AMB=∠D=60°。


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
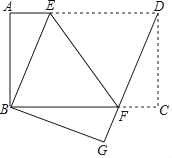
【题目】在矩形纸片ABCD中,AB=6,BC=8,现将纸片折叠,使点D与点B重合,折痕为EF,连接DF.
(1)说明△BEF是等腰三角形;
(2)求折痕EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
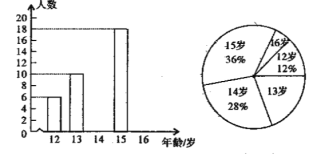
【题目】某中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.依据以下信息解答问题:
(1)此次共调查了多少人?
(2)求“年龄![]() 岁”在扇形统计图中所占圆心角的度数;
岁”在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长方体,它的长、宽、高分别为![]() 、
、![]() 、
、![]() .
.![]() 和
和![]() 是这个长方体上两个相对的顶点,点
是这个长方体上两个相对的顶点,点![]() 处有一只蚂蚁,想到点
处有一只蚂蚁,想到点![]() 处去吃可口的食物,则蚂蚁沿着长方体表面爬行到点
处去吃可口的食物,则蚂蚁沿着长方体表面爬行到点![]() 的最短路程为__________
的最短路程为__________![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
(1)操作发现:如图1,点D是等边△ABC边BA上一动点(点D与点B不重合),连结DC,以DC为边在CD上方作等边△DCE,连结AE.你能发现线段AE与BD之间的数量关系吗? 证明你发现的结论.
(2)类比猜想:如图2,当动点D运动至等边△ABC边BA的延长线上时,其余条件不变,猜想:(1)中的结论是否成立,不用说明理由.
(3)拓展探究:如图3,当动点D在等边△ABC边BA上运动时(点D与点B不重合),连结 DC,以DC为边在CD上方和下方分别作等边△DCE和等边△DCE′,连结AE、BE′,探究:AE、BE′与AB有何数量关系?并说明理由.
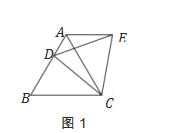
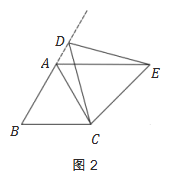

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=90°,BC=6,直线MN∥BC,且分别交边AB,AC于点M,N,已知直线MN将△ABC分为面积相等的两部分.如果将线段AM绕着点A旋转,使点M落在边BC上的点D处,那么BD=________.
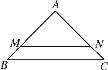
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,![]() ),B(﹣1,m)是一次函数y=kx+b与反比例函数y=
),B(﹣1,m)是一次函数y=kx+b与反比例函数y=![]() 图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(1)求m的值及一次函数解析式;
(2)P是线段AB上的一点,连接PC、PD,若△PCA和△PDB面积相等,求点P坐标.
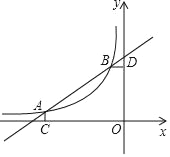
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚C处测得一座建筑物顶点A的仰角为63.4°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为53°.已知BC=90米,且B、C、D在同一条直线上,山坡坡度i=5:12.
(1)求此人所在位置点P的铅直高度.(结果精确到0.1米)
(2)求此人从所在位置点P走到建筑物底部B点的路程(结果精确到0.1米)
(测倾器的高度忽略不计,参考数据:tan53°≈![]() ,tan63.5°≈2)
,tan63.5°≈2)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com