
【题目】随着城际铁路的开通,从甲市到乙市的高铁里程比快里程缩短了90千米,运行时间减少了8小时,已知甲市到乙市的普快列车里程为1220千米,高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)若从甲市到乙市途经丙市,且从甲市到丙市的高铁里程为780千米.某日王老师要从甲市去丙市参加14:00召开的会议,如果他买了当日10:00从甲市到丙市的高铁票,而且从丙市高铁站到会议地点最多需要0.5小时.试问在高铁列车准点到达的情况下,王老师能否在开会之前赶到会议地点?
【答案】(1)高铁列车的平均时速为240千米/小时;(2)王老师能在开会之前到达.
【解析】
(1)设普快的平均时速为x千米/小时,高铁列车的平均时速为2.5x千米/小时,根据题意可得,高铁走(1220-90)千米比普快走1220千米时间减少了8小时,据此列方程求解;
(2)求出王老师所用的时间,然后进行判断.
解:(1)设普快的平均时速为x千米/小时,高铁列车的平均时速为2.5x千米/小时,
由题意得,![]() ,
,
解得:x=96,
经检验,x=96是原分式方程的解,且符合题意,
则2.5x=240,
答:高铁列车的平均时速为240千米/小时;
(2)780÷240=3.25,
则坐车共需要3.25+0.5=3.75(小时),
从10:00到下午14:00,共计4小时>3.75小时,
故王老师能在开会之前到达.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
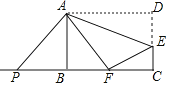
【题目】如图,矩形ABCD中,AB=12,AD=15,E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处,点P是线段CB延长线上的动点,连接PA,若△PAF是等腰三角形,则PB的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
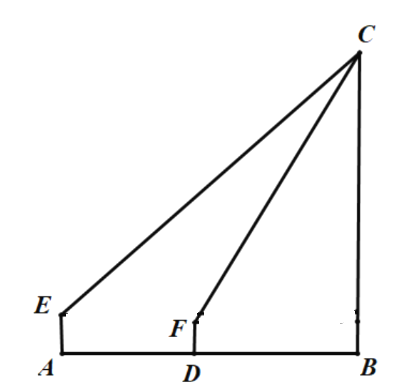
【题目】清代《修武县志》有胜果寺的记载,“康熙五十二年三月十七日,塔顶现青白二气如云,越二日乃止”,此文中的塔即为“胜果寺塔”,是修武作为“千年古县”的标志性古建筑.为了测量塔的高度,某校数学兴趣小组的两名同学采用了如下方式进行测量.如图,小明站在![]() 处,眼睛
处,眼睛![]() 距离地面的高度为
距离地面的高度为![]() ,测得塔顶
,测得塔顶![]() 的仰角为
的仰角为![]() ,小红站在距离小明
,小红站在距离小明![]() 的
的![]() 处,眼睛
处,眼睛![]() 距离地面的高度为
距离地面的高度为![]() ,测得塔顶
,测得塔顶![]() 的仰角为
的仰角为![]() ,已知
,已知![]() ,
,![]() ,塔底
,塔底![]() 在同一水平面上,由此即可求出塔高
在同一水平面上,由此即可求出塔高![]() .你知道是怎么求的吗?请写出解题过程.(结果精确到
.你知道是怎么求的吗?请写出解题过程.(结果精确到![]() .参考数据:
.参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
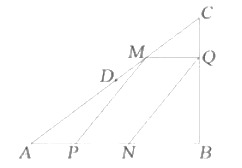
【题目】如图,在![]() 中,
中,![]() 为边
为边![]() 的中点.点
的中点.点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 运动到点
运动到点![]() 停止,同时点
停止,同时点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿折线
个单位长度的速度沿折线![]() 运动到点
运动到点![]() 停止,当点
停止,当点![]() 停止运动时,点
停止运动时,点![]() 也停止运动.当点
也停止运动.当点![]() 不与
不与![]() 的顶点重合时,过点
的顶点重合时,过点![]() 作
作![]() 交
交![]() 的边于点
的边于点![]() 以
以![]() 和
和![]() 为边作
为边作![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() (秒),
(秒),![]() 的面积为
的面积为![]() (平方单位).
(平方单位).
(1)当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值;
的值;
(2)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(3)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)连结![]() 直接写出
直接写出![]() 将
将![]() 分成面积相等的两部分时
分成面积相等的两部分时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
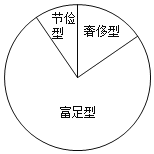
【题目】某校为了解学生零用钱支出情况,从七、八、九年级800名学生中随机抽取部分学生,对他们今年5月份的零用钱支出情况进行调查统计,并绘制成如下统计图表:
组别 | 零用钱支出x(单位:元) | 频数(人数) | 频率 | |
节俭型 | 一 | x<20 | m | 0.05 |
二 | 20≤x<30 | 4 | a | |
富足型 | 三 | 30≤x<40 | n | 0.45 |
四 | 40≤x<50 | 12 | b | |
奢侈型 | 五 | x≥50 | 4 | c |
合计 | 1 | |||
(1)表中a+b+c= ;m= ;本次调查共随机抽取了 名同学;
(2)在扇形统计图中,“富足型”对应的扇形的圆心角的度数是 ;
(3)估计今年5月份全校零花钱支出在30≤x<40范围内的学生人数;
(4)在抽样的“奢侈型”学生中,有2名女生和2名男生.学校团委计划从中随机抽取2名同学参加“绿苗理财计划”活动,请运用树状图或者列表说明恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答年新型冠状病毒防治全国统一考试全国卷试卷满分![]() 分,社区管理员随机从有
分,社区管理员随机从有![]() 人的某小区抽取
人的某小区抽取![]() 名人员的答卷成绩,根据他们的成绩数据绘制了如下的表格和统计图:
名人员的答卷成绩,根据他们的成绩数据绘制了如下的表格和统计图:
等级 | 成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
| |
根据上面提供的信息,回答下列问题: .
(1)统计表中的![]() ,
,![]() ,
,![]() ;
;
(2)请补全条形统计图;
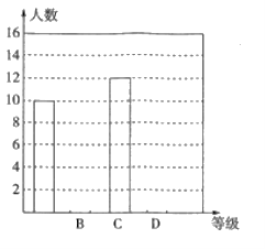
(3)根据抽样调查结果,请估计该小区答题成绩为“![]() 级”的有多少人?
级”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在九年级“线上教学”结束后,为了了解学生的视力情况,抽查了部分学生进行视力检查.根据检查结果,制作下面不完整的统计图表.

(1)求组别C的频数m的值.
(2)求组别A的圆心角度数.
(3)如果势视力值4.8及以上属于“视力良好”,请估计该市25000名九年级学生达到“视力良好”的人数,根据上述图表信息,你对视力保护有什么建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,抛物线C1:y1=x2-2mx+2m2-1,抛物线C2:y2=x2-2nx+2n2-1,
(1)若m=2,过点A(0,7)作直线l垂直于y轴交抛物线C1于点B、C两点.
①求BC的长;
②若抛物线C2与直线l交于点E、F两点,若EF长大于BC的长,直接写出n的范围;
(2)若m+n=k(k是常数),
①若![]() ,试说明抛物线C1与抛物线C2的交点始终在定直线上;
,试说明抛物线C1与抛物线C2的交点始终在定直线上;
②求y1+y2的最小值(用含k的代数式表示) .
查看答案和解析>>
科目:初中数学 来源: 题型:
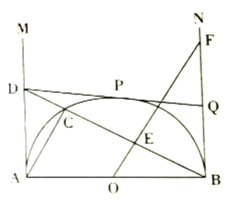
【题目】如图,![]() 是半圆
是半圆![]() 的直径,
的直径,![]() ,射线
,射线![]() 为半圆
为半圆![]() 的切线.在
的切线.在![]() 上取一点
上取一点![]() ,连接
,连接![]() 交半圆
交半圆![]() 于点
于点![]() ,连接
,连接![]() .过点
.过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,与
,与![]() 相交于点
相交于点![]() .过点
.过点![]() 作半圆的切线
作半圆的切线![]() ,切点为
,切点为![]() ,与
,与![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)当![]() 与
与![]() 的面积相等时,求
的面积相等时,求![]() 的长;
的长;
(3)求证:当![]() 在
在![]() 上移动时(
上移动时(![]() 点除外),点
点除外),点![]() 始终是线段
始终是线段![]() 的中点.
的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com